Penrose pone las bases de la gravedad cuántica

Roger Penrose es uno de los nuevos humanistas del siglo que se ha interesado por los problemas de las matemáticas, de la física, de la biología, de la psicología y de la filosofía. Siguiendo el modelo de Popper de los tres mundos, ha trabajado sobre la flecha del mundo 1 de la física, al mundo 2 de la conciencia, y del mundo 3 de las matemáticas, al mundo 1.

En esta última dirección ha publicado numerosos libros y artículos, donde aborda la asignatura pendiente de la unificación de la mecánica cuántica y la teoría del campo gravitatorio. El camino que ha seguido Penrose es encontrar una base común a ambas.

Para ello ha introducido dos modelos: los "spin networks" y los "twistors", el primero discreto, con una métrica intrínseca, no relativista, previo al concepto de espacio, el segundo continuo, con una métrica extrínseca, relativista e inmerso en un espacio-tiempo dado.

Con estos modelos intenta Penrose responder a la pregunta sobre el "por qué" de la realidad física, en vez del "cómo". Nos encontramos así ante uno de los grandes misterios de la razón humana que nos acercan al misterio de Dios.

Asignatura pendiente

La asignatura pendiente de la física teórica del siglo XX ha sido la unificación de la relatividad general y la mecánica cuántica. Las aproximaciones que se han hecho van desde la cuantificación canónica del campo gravitatorio hasta la ampliación de las simetrías en la teoría de supercuerdas.

Existen también teorías que buscan una nueva interpretación de las teorías del espacio-tiempo, como se vio en el congreso sobre la ontología del espacio-tiempo que tuvo lugar en junio de 2006 en Montreal, y del que se informó ampliamente en Tendencias21, en la sección “tendencias de las religiones”: El enigma del espacio-tiempo sigue apasionando a los físicos y filósofos.

Esta dirección, profundizar en las estructuras del espacio-tiempo, ha sido seguida por el físico teórico Roger Penrose, cuyas ideas han sido presentadas en numerosos artículos y libros (entre ellos "La nueva mente del Emperador", “Las sombras de la mente", "La naturaleza del espacio y tiempo", "El camino a la Realidad").

Penrose es actualmente Profesor emérito de Matemáticas de la Universidad de Oxford, y ya en los años 60 presentó su teoría de los "spin networks" que después fue tomada por Ashtekar y Rovelli, y otros, en la teoría de la gravitación cuántica.

A partir de los años 70, Penrose presentó su teoría de los "twistor", que algunos físicos han aplicado a la teoría de las supercuerdas para resolver el enigma de las 11 dimensiones del espacio-tiempo. En su último libro "El camino a la Realidad" Penrose ha reivindicado la paternidad de las teorías de los "spin networks" y de los "twistors" que se empieza a utilizar por los físicos teóricos y que nosotros vamos a resumir brevemente.

El continuo en física

El continuo juega un papel muy importante en física. En primer lugar se da el continuo real del espacio-tiempo de cuatro dimensiones, donde tienen lugar los fenómenos del universo. Por otro lado, encontramos el continuo complejo de la mecánica cuántica, que sirve de soporte al concepto de amplitud de probabilidad y a la ley de superposición de estados en un espacio de Hilbert. Se supone que ambos continuos, uno real y otro complejo, son diferentes en naturaleza y pueden existir independientemente uno de otro. El espacio de la mecánica cuántica se ha impuesto al espacio de la mecanica clásica.

Se puede encontrar una interrelación entre los números complejos de la mecánica cuántica y la estructura del espacio-tiempo que ayudaría a unificar los dos espacios. Los estados de spin de una partícula de spin 1/2 son combinaciones lineales de dos estados "spin hacia arriba" y "spin hacia abajo", que también se podían llamar "spin a la derecha" y “spin a la izquierda" o "spin hacia adelante" y “spin hacia atrás".

Pero para conseguir todas las direcciones posibles en un espacio de tres dimensiones, es necesario tomar todas las combinaciones complejas de los dos estados originales. Por consiguiente, existe una relación íntima entre el espacio de tres dimensiones y los números complejos.

Espacio-tiempo discreto

El uso del continuo en física se basa en su utilidad matemática y en su desarrollo más avanzado que las matemáticas discretas. Penrose propone que las leyes de la física sean expresadas en términos de principios combinatorios; es decir, en términos de procesos finitos, tales como contar con números enteros o con fracciones de números enteros, como son las leyes de probabilidad.

Esto aparece ya en las propiedades de la onda de probabilidad de la mecánica cuántica, y en los valores discretos de los valores propios de ciertos observables cuánticos. "Mi idea -dice Penrose- es intentar reformular las leyes de la física de manera que puedan ser expresadas en términos de cantidades discretas según la mecánica cuántica...

De este modo la teoría cuántica y la teoría del espacio-tiempo resultarían proceder conjuntamente de una teoría más fundamental de caracter combinatorio”. Ahora bien, tenemos el dilema de cuál va a ser el primero en una teoría unificada. La respuesta de Penrose es clara: el espacio discreto de la mecánica cuántica, del cual surgirá la geometría del espacio continuo de la mecánica cuántica.

En particular, Penrose construye su espacio clásico a partir de los valores discretos del momento angular de un conjunto de partículas que interaccionan entre si, y que no se encuentran colocados en ningún espacio: "mi modelo es funcional con objetos y sus relaciones mutuas. Un objeto está colocado, en dirección o en posición, en términos de sus relaciones con otros objetos. Uno no necesita un espacio para comenzar. El concepto de espacio aparece al final como una conveniencia".

El modelo de los "spin networks" de Penrose

La magnitud cuántica que propone Penrose para reconstruir el espacio clásico debe poseer las siguientes propiedades: i) debe ser discreta; ii) debe estar referida a una direccón espacial; iii) no ha de suponer un espacio preliminar.

Una magnitud que cumple estas condiciones es el momento angular total: sus valores propios están discretizados y su magnitud es intrínseca al sistema. Ahora tomamos todo o parte del universo físico constituido por sistemas elementales o particulares, cada uno con momento angular total y todos interaccionando entre sí, formando una red de spines, llamada spin network.

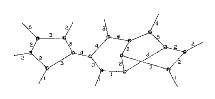
Cada segmento lineal (ver figura) representa un objeto físico o "unidad" cuyo momento angular total se recombina con otro momento angular, cumpliendo las leyes de la mecánica cuántica. La finalidad del modelo es construir un concepto de espacio físico utilizando solamente las reglas cuánticas de los diagramas. Estas reglas son puramente combinatorias y nos permiten calcular las probabilidades del diagrama para varios valores del spin total que puede ocurrir cuando una nueva línea se añade al modelo.

Estas probabilidades son números racionales, y a partir de estas se puede construir un concepto geométrico de espacio, suponiendo que estos segmentos del "spin network" con valores de spin muy alto N definen una dirección en el espacio. Más explícitamente se diría que la proyección del spin N sobre esa dirección produce (2N + 1) valores diferentes y discretos, de modo que cuanto mas grande sea N mejor definida está la dirección. Entre dos direcciones de valores de spin muy grandes, N y M, se puede definir un ángulo cuya probabilidad se calcula por medio de reglas combinatorias. Si las direcciones N y M son suficientemente rígidas, la geometría que se obtiene coincide (con un grado de aproximación bastante grande) con la geometría euclídea de dimensión 3.

Este es el objetivo que Penrose quería obtener para la geometría física a partir de las propiedades discretas de la mecánica cuántica. Y ésta es la geometría real que nosotros observamos, aunque a comienzo del proceso se hayan utilizado variables continuas clásicas (como, por ejemplo, las coordenadas esféricas o polares) las cuales desaparecen una vez obtenidos los valores discretos de los operadores cuánticos. De nuevo, para Penrose, el espacio discreto de la mecánica cuántica tiene preferencia real sobre el espacio continuo de la mecánica cuántica.

El modelo relativista de los "twistors"

El modelo de los "spin networks" es no-relativista, porque el momento angular utilizado tiene tres componentes solamente. Habría que añadir al espacio de tres dimensiones, construido a partir de los "spin networks", una cuarta dirección temporal para que el modelo fuese relativista. Pero además el modelo es estacionario. Las partículas intercambian los spines pero no se mueven.

Recordemos que el momento angular total está compuesto de una componente spinorial y una componente orbital; esta última producto vectorial de los vectores posición y momento. Si la componente orbital es distinta de cero, significa que las partículas se mueven, y por consiguiente hay que tener en cuenta las posiciones y desplazamientos entre partículas. Consideremos dos partículas en movimiento relativo. Supongamos que se combinan formando un nuevo sistema con un momento angular total. Este está compuesto de la componente spinorial y orbital de ambas partículas.

Para facilitar el cálculo podemos usar la base de los spines para describir las propiedades del momento angular orbital en función de esta base. Pero esto tiene la dificultad de que la componente orbital está compuesta de magnitudes continuas y la componente spinorial de magnitudes discretas.

La solución, dice Penrose, es tomar el límite de las cantidades discretas, porque entonces ambas magnitudes serían continuas. Para un número pequeño de partículas, se distingue la componente spinorial y la componente orbital, pero cuando el número de partículas se hace muy grande ambos conceptos tienden a homogeneizarse.

Un álgebra compleja para los "twistors"

La motivación de Penrose para construir los twistors fue hacer una generalización de los spin networks de modo que el modelo fuese relativista. Por consiguiente,más de acuerdo con la realidad, ya que las componentes del momento angular y del momento lineal serían más homogéneas y además complejas para cumplir los requisitos de la mecánica cuántica. Estas condiciones las cumplían los "twistors" porque:

a) en la relatividad especial la posición de una partícula se representa por cuatro números reales que forman un vector (una coordenada temporal y tres espaciales). Para el momento lineal se necesitan también 4 coordenadas espacio-temporales. Los "twistors" son también vectores de cuatro componentes complejas que se pueden hacer corresponder con las ocho componentes reales del vector posición y el vector momento.

b) el momento angular y lineal de una partícula se puede escribir en función de ciertas combinaciones de "twistors" de igual naturaleza.

c) los "twistors" representan también estados como en la mecánica cuántica, y satisfacen las reglas de conmutación canónicas. Juegan también el papel de autovectores donde operan ciertos operadores que representan ciertas magnitudes físicas como la masa o el spin. De este modo los "twistors" son objetos matemáticos de cuatro componentes complejas que constituyen la base para describir la mecánica cuántica con soporte en la relatividad especial y sobre todo en la relatividad general.

Los "twistors" y la relatividad general

Los "twistors" que acabamos de describir representan sistemas o partículas elementales de masa nula y spin entero o semientero, momento lineal y momento angular determinado, que se desarrollan en el tiempo según las leyes de la relatividad especial. El espacio-tiempo subyacente de Minkowski es plano, es decir, tiene curvatura cero. Las partículas de masa no nula se obtienen por integración respecto a las variables complejas de varias partículas de masa nula.

El problema que se plantea Penrose es la generalización de este modelo a la relatividad general, donde el espacio-tiempo no es plano, es decir, tiene curvatura distinta de cero. ¿Cómo resolver este problema? Supongamos que tenemos un conjunto de "twistors" donde hemos calculado ciertas magnitudes como el momento lineal, el momento angular y la probabilidad de que estos evolucionen en el tiempo. Estos cálculos conducirían a una geometría local de tipo Minkowski.

Si esto se cumpliese para varios conjuntos diferentes situados en puntos diferentes del espacio-tiempo global, las geometrías locales resultantes no serían, en general, consistentes unas con otras. La medida de un punto espacio-temporal de una región minkowskiana aparecería difusa vista desde otra región minkowskiana del espacio-tiempo.

Matemáticamente esto supondría que hemos realizado una transformación de las propiedades de un sistema con un espacio-tiempo plano a otro espacio-tiempo plano diferente, pero el espacio-tiempo global que abarca a los dos no es plano, sino que es difuso respecto de los dos sistemas locales, y esta difusión se traduce en el modelo de Penrose en la curvatura no nula del espacio-tiempo global.

"Spin networks" y gravedad cuántica

El modelo de los "twistors" se ha aplicado con éxito a la clasificación de las partículas elementales y a la formulación de la relatividad general. Pero recientemente algunos modelos de la gravedad cuántica han retomado la idea de los "spin networks" de Penrose para desarrollar un modelo discreto llamado loop quantum gravity donde el espacio subyacente está discretizado.

Esta idea de las magnitudes discretas en física fue ya propuesta por Schrödinger, Einstein, Snyder, Ahmavaara y otros. El mismo Penrose reconoce que él también era favorable a una discretización del espacio, ya que éste era un concepto derivado de las propiedades combinatorias de los "spin neetworks" y, aunque luego desarrolló más en profundidad el modelo continuo de los "twistors", no ha querido renunciar al modelo de los "spin networks" pue él había introducido en los años 60.

En su última obra, El camino a la Realidad, Penrose recoge los desarrollos de la gravedad cuántica que han utilizado sus ideas: "loop quantum gravity" de Ashtekar (utilizando unas nuevas variables de campo se construye una acción definida sobre los grafos que se derivan de los "spin networks”); el calculo de Regge (que discretiza el espacio con una triangulación que da origen a tetraedros en cuyas caras se adjuntan los símbolos de Wigner para calcular la función de partición del campo gravitatorio); los "causal sets" de Sorkin y las “quantum causal histories" de Markopoulou (utilizando el principio de causalidad, construyen sistemas causales de eventos que forman una red discreta que representan las interacciones cuánticas); los "spin foams" de Smolin y Rovelli, (que generalizan los modelos de Regge en tres dimensiones a cuatro, descomponiendo el espacio-tiempo en simplices donde se calcula la función de partición).

El camino hacia la realidad

En su último libro, Penrose se pregunta si el conocimiento del Universo tan espectacular que ha conseguido la ciencia en los últimos siglos ha conseguido desvelarnos la realidad de las cosas, su esencia y estructura más profunda. La respuesta, dice Penrose, es negativa. La ciencia descubre el cómo de las cosas, no llega al "qué" ni al "por qué" de las cosas.

Para responder a esta pregunta filosófica Penrose acude a su coetáneo Popper en su famosa hipótesis de los tres mundos, dándole una interpretación original. El mundo 1, o de la física, que abarca todos los fenómenos naturales que se observan por los sentidos. El mundo 2, o de la conciencia, que recoge las percepciones y juicios de observación que el entendimiento humano construye con los datos de los sentidos. El mundo 3, o de las verdades absolutas y eternas, principalmente las verdades matemáticas, que se encuentran fuera de la mente humana, después que ésta las ha descubierto. El tercer mundo es una versión moderna de las ideas universales de Platón, aplicado a los modelos matemáticos de las teorías modernas de la física.

Existen unas relaciones entre los tres mundos, de modo que el mundo 1 influye en el mundo 2, y éste en el mundo 3, que a su vez influye en el mundo 1, como lo hacen los objetos platónicos universales en los objetos particulares del mundo de "la caverna".

Penrose ha dedicado varios libros a estudiar la flecha 1-2, en los que defiende la emergencia de la conciencia respecto del mundo físico, pero en su libro "El camino hacia la realidad" ha destacado la flecha 3-1, donde ha defendido el caracter universal de los objetos matemáticos y su influjo en las teorías científicas. Sin embargo, el camino para entender la realidad física como conocimiento objetivo del mundo que nos rodea no está todavía acabado. A lo más que puede aspirar una teoría física es a encontrar las leyes matemáticas que se ajusten a los hechos.

Siguiendo el esquema de los tres mundos, Penrose presenta su propia posición, según la cual en mundo 3 proporciona una cierta "realidad" a los conceptos matemáticos, pero él mismo se retrae de intentar la identificación de la realidad física con la realidad abstracta del mundo 3 o mundo de las ideas universales de Platón.

Cada uno de los tres mundos tiene su propia realidad, aunque cada uno esté fundado en el que le precede. Este comportamiento cíclico de los tres mundos es, para Penrose, un misterio pero, sin embargo, nos acerca más al misterio de Dios.


Miguel Lorente, Catedrático Emérito de Física en la Universidad de Oviedo, es miembro de la Cátedra CTR.