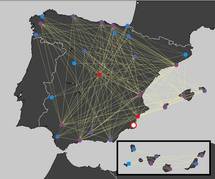
Red de conexiones aéreas entre aeropuertos en España. La figura representa las probabilidades de dispersión de, por ejemplo, una enfermedad o una moda, desde un punto hacia el resto de la red. Rojo: alta probabilidad de dispersión. Azul: probabilidad baja. Imagen: J. Fernandez-Gracia, P. Fleurquin, M.A. Tugores.
Un estudio en el que ha participado el Consejo Superior de Investigaciones Científicas (CSIC) ha desarrollado una metodología que permite clasificar los elementos de una red en función de su importancia para el funcionamiento del sistema.
Combinando los datos correspondientes a la dinámica de la red y estructura, un logaritmo matemático señala los nodos más “influyentes”, aquellos cuya actividad determina el éxito del sistema. El artículo ha sido publicado en el último número de la revista Scientitic Reports.
Algoritmo matemático aplicado a dinámicas de red
La idea es similar a la que rige los buscadores de Internet, que analizan y seleccionan las entradas más relevantes de cada tema. “En este caso hemos aplicado un algoritmo matemático a las dinámicas y mecanismos habituales de una red.
El resultado es una clasificación ordenada de los puntos de conexión con mayor peso”, explica el investigador del CSIC, Víctor Eguíluz, del Instituto de Física Interdisciplinar y Sistemas Complejos, centro mixto del CSIC y la Universidad de las Islas Baleares.
Muchos procesos se propagan a través de redes de interacción complejas, como las enfermedades, la información, etc.
Combinando los datos correspondientes a la dinámica de la red y estructura, un logaritmo matemático señala los nodos más “influyentes”, aquellos cuya actividad determina el éxito del sistema. El artículo ha sido publicado en el último número de la revista Scientitic Reports.
Algoritmo matemático aplicado a dinámicas de red
La idea es similar a la que rige los buscadores de Internet, que analizan y seleccionan las entradas más relevantes de cada tema. “En este caso hemos aplicado un algoritmo matemático a las dinámicas y mecanismos habituales de una red.
El resultado es una clasificación ordenada de los puntos de conexión con mayor peso”, explica el investigador del CSIC, Víctor Eguíluz, del Instituto de Física Interdisciplinar y Sistemas Complejos, centro mixto del CSIC y la Universidad de las Islas Baleares.
Muchos procesos se propagan a través de redes de interacción complejas, como las enfermedades, la información, etc.
“La ventaja de conocer los puntos más importantes del recorrido es el ahorro de esfuerzos, tanto para potenciar como para bloquear el proceso. Por ejemplo, si conoces la red a través de la cual se transmite una enfermedad y tienes un número limitado de vacunas, puedes saber dónde tienes que aplicarlas para conseguir que la enfermedad se extienda lo menos posible”, comenta el investigador.
Los resultados obtenidos con la metodología desarrollada en este estudio, afirman los investigadores, cuantifican en qué medida puede controlarse la eficiencia de un sistema manipulando sólo un nodo.
Un caso paradigmático de este aspecto es el tráfico aéreo. Cuando un aeropuerto sufre retrasos en sus vuelos, en función de su relevancia dentro del sistema, los demás aeropuertos lo notarán más o menos.
Por el momento, las conclusiones de este trabajo son solo teóricas. Los investigadores se han basado en las dinámicas de sistemas complejos descritos en otros estudios ya publicados.
Los resultados obtenidos con la metodología desarrollada en este estudio, afirman los investigadores, cuantifican en qué medida puede controlarse la eficiencia de un sistema manipulando sólo un nodo.
Un caso paradigmático de este aspecto es el tráfico aéreo. Cuando un aeropuerto sufre retrasos en sus vuelos, en función de su relevancia dentro del sistema, los demás aeropuertos lo notarán más o menos.
Por el momento, las conclusiones de este trabajo son solo teóricas. Los investigadores se han basado en las dinámicas de sistemas complejos descritos en otros estudios ya publicados.

 Tendencias Científicas
Tendencias Científicas

 La Inteligencia Artificial puede ver a través del espejo
La Inteligencia Artificial puede ver a través del espejo CIENCIA ON LINE
CIENCIA ON LINE