Simulan en 3-D ondas 'invisibles' del océano

Basura, nutrientes y pequeños animales son arrastrados, suspendidos en los océanos del mundo, por ondas invisibles a simple vista, según un nuevo modelo en 3-D desarrollado por matemáticos de la Universidad de Waterloo (Canadá).

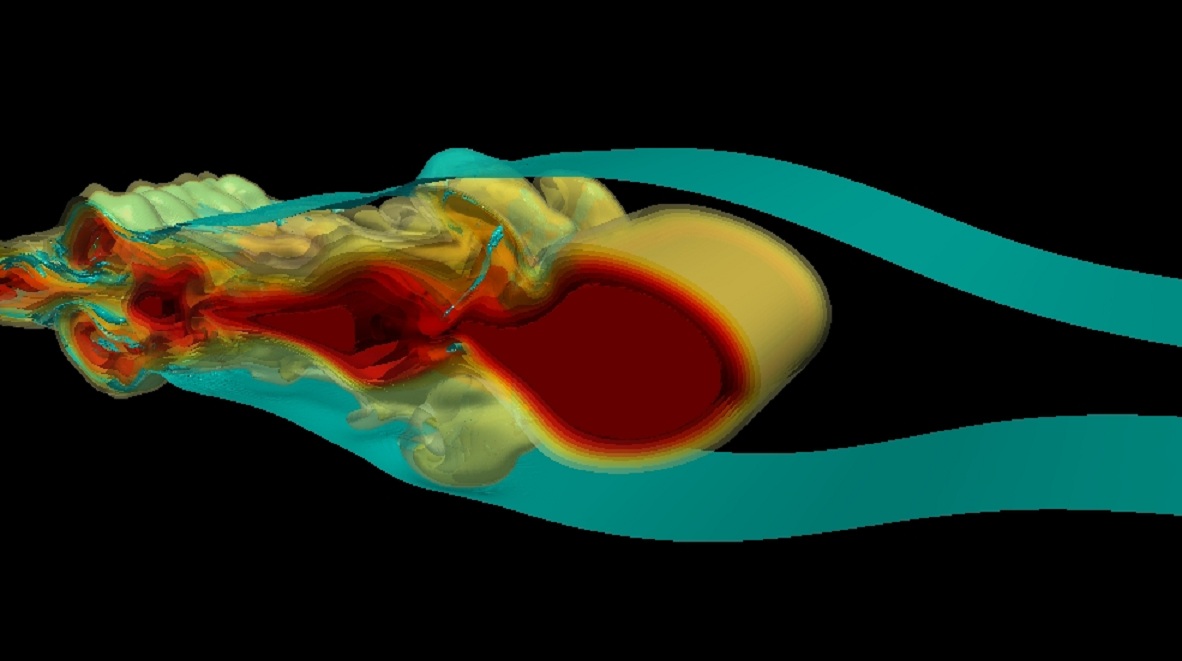
David Deepwell, estudiante de posgrado, y el profesor Marek Šťastná, de la Facultad de Matemáticas de Waterloo, han creado una simulación en 3-D que muestra cómo materiales como fitoplancton, contaminantes y nutrientes se mueven dentro de los ecosistemas acuáticos a través de protuberancias bajo el agua llamadas ondas internas de modo-2.

La simulación puede ayudar a los investigadores a entender cómo pueden las ondas internas transportar materiales a través de largas distancias. Su modelo se presentó en la revista Physics of Fluids, del Instituto Americano de Física, a principios de la semana pasada.

En la simulación, líquidos de diferentes densidades se colocan en capas como las capas de una tarta, creando un entorno similar al que se encuentra en grandes masas de agua como lagos y océanos. Se crea una capa media de fluido, conocida como picnoclina, sobre la que las capas se amontonan estrechamente, y es en esta capa donde los materiales tienden a ser capturados.

"Cuando el fluido que hay detrás de la barrera se mezcla y a continuación se retira la barrera, el fluido mezclado colapsa en la estratificación porque es más pesado que la capa superior y más ligero que el de abajo", explica Deepwell en la nota de prensa de la universidad.

Colorante

"Añadiendo colorante al fluido mezclado mientras que la barrera está en su lugar simula el material que queremos que transporten las ondas de modo-2 -las protuberancias formadas en la picnoclina una vez que la barrera se quita-. Entonces podemos medir el tamaño de la onda, la cantidad de colorante que queda atrapada dentro de ella y lo bien que la onda lleva el material capturado".

Deepwell y Statsna encontraron que cuanto mayor sea la protuberancia dentro de la picnoclina, mayor será la cantidad de material transportado por la onda de modo-2.

Si bien han descubierto un escenario óptimo en el que la onda interna de modo-2 sobrevive y luego transporta material a la mayor distancia posible, las ondas internas también pueden romperse debido a pequeñas regiones de inestabilidad, llamadas inestabilidades de sotavento, que se forman detrás de la onda.

Cuando la onda de modo-2 se rompe, el material se pierde detrás de ella. Trabajos y simulaciones experimentales en curso están explorando cómo interactúa este tipo de onda con la topografía submarina, como montes submarinos.

Referencia bibliográfica:

David Deepwell, Marek Stastna: Mass transport by mode-2 internal solitary-like waves. Physics of Fluids (2016). DOI: 10.1063/1.4948544.