
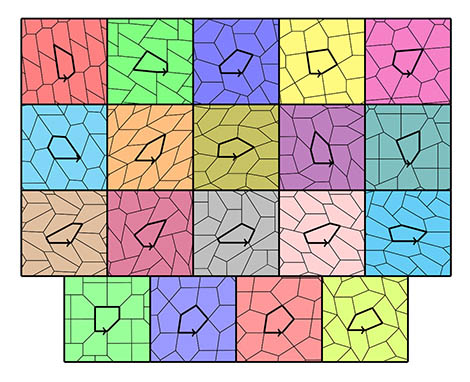
Los 15 tipos de pavimentación pentagonales y los 4 tipos particulares. © Michael Rao, Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS de Lyon/Université Claude Bernard Lyon 1).
Cubrir una superficie plana con un motivo único es un problema matemático que intriga a la humanidad desde la antigüedad, especialmente por la calidad estética de los pavimentos, como los mosaicos y los azulejos.
Uno de los problemas sin resolver en este campo, que cuestiona a la comunidad científica desde 1918, se ha resuelto ya definitivamente a través de la informática: sólo hay 15 tipos de pentágonos que pueden embaldosar una habitación infinita.
Para recubrir un suelo con una única y misma forma geométrica existen varias fórmulas: triángulos, cuadrados, rectángulos, hexágonos, etc. La investigación exhaustiva de todas las formas convexas que pueden pavimentar un piso, es decir, unas formas con ángulos inferiores a 180º y que permiten recubrir toda la superficie sin que falte ni sobre ningún espacio, fue iniciada por Karl Reinhardt en 1918.
En aquel entonces estableció que todos los triángulos y cuadriláteros pueden pavimentar un plano, que sólo 3 hexágonos lo consiguen y que un polígono de 7 lados o más no permiten recubrir un piso sin fisuras. La explicación matemática es que son los únicos cuyos ángulos internos son divisores de 360 grados. Sólo quedaba pendiente el número de pentágonos necesario.
Desde 1918 y hasta 2015, se han descubierto 15 tipos de pentágonos, pero todavía no se sabía si podían existir nuevas figuras pentagonales capaces de teselar un plano.
Ahora, Michaël Rao, investigador del CNRS (Francia), ha demostrado definitivamente que sólo existe un número finito de familias de pentágonos capaces de conseguirlo, informa el CNRS en un comunicado. Una familia es un conjunto de condiciones que se basan únicamente en los ángulos de un pentágono.
Generando todas las posibilidades a través de un programa informático, ha descubierto que 371 familias de pentágonos pueden potencialmente recubrir un plano.
La exhaustividad de esta lista fue verificada, de manera independiente, por Thomas Hales, que probó la conjetura de Kepler por ordenador. Esta conjetura afirma que si apilamos esferas iguales, la densidad máxima se alcanza con un apilamiento piramidal de caras centradas. Esta densidad es aproximadamente del 74 %.
A continuación, apoyándose también en la informática, Rao testó cada una de las familias de pentágonos que reúnen las condiciones necesarias para cubrir un plano y descubrió que sólo 19 familias lo consiguen, tanto por sus ángulos como por sus lados.
Y que entre esas 19 familias, sólo15 corresponden a los tipos ya conocidos, ya que los otros cuatro restantes son casos particulares derivados de esos 15. En consecuencia, concluye que sólo 15 tipos de pentágono son los únicos capaces de cubrir sin fisuras una superficie plana. Con esta metodología, Michael Rao ha resuelto un problema matemático de más de cien años de antigüedad.
Uno de los problemas sin resolver en este campo, que cuestiona a la comunidad científica desde 1918, se ha resuelto ya definitivamente a través de la informática: sólo hay 15 tipos de pentágonos que pueden embaldosar una habitación infinita.
Para recubrir un suelo con una única y misma forma geométrica existen varias fórmulas: triángulos, cuadrados, rectángulos, hexágonos, etc. La investigación exhaustiva de todas las formas convexas que pueden pavimentar un piso, es decir, unas formas con ángulos inferiores a 180º y que permiten recubrir toda la superficie sin que falte ni sobre ningún espacio, fue iniciada por Karl Reinhardt en 1918.
En aquel entonces estableció que todos los triángulos y cuadriláteros pueden pavimentar un plano, que sólo 3 hexágonos lo consiguen y que un polígono de 7 lados o más no permiten recubrir un piso sin fisuras. La explicación matemática es que son los únicos cuyos ángulos internos son divisores de 360 grados. Sólo quedaba pendiente el número de pentágonos necesario.
Desde 1918 y hasta 2015, se han descubierto 15 tipos de pentágonos, pero todavía no se sabía si podían existir nuevas figuras pentagonales capaces de teselar un plano.
Ahora, Michaël Rao, investigador del CNRS (Francia), ha demostrado definitivamente que sólo existe un número finito de familias de pentágonos capaces de conseguirlo, informa el CNRS en un comunicado. Una familia es un conjunto de condiciones que se basan únicamente en los ángulos de un pentágono.
Generando todas las posibilidades a través de un programa informático, ha descubierto que 371 familias de pentágonos pueden potencialmente recubrir un plano.
La exhaustividad de esta lista fue verificada, de manera independiente, por Thomas Hales, que probó la conjetura de Kepler por ordenador. Esta conjetura afirma que si apilamos esferas iguales, la densidad máxima se alcanza con un apilamiento piramidal de caras centradas. Esta densidad es aproximadamente del 74 %.
A continuación, apoyándose también en la informática, Rao testó cada una de las familias de pentágonos que reúnen las condiciones necesarias para cubrir un plano y descubrió que sólo 19 familias lo consiguen, tanto por sus ángulos como por sus lados.
Y que entre esas 19 familias, sólo15 corresponden a los tipos ya conocidos, ya que los otros cuatro restantes son casos particulares derivados de esos 15. En consecuencia, concluye que sólo 15 tipos de pentágono son los únicos capaces de cubrir sin fisuras una superficie plana. Con esta metodología, Michael Rao ha resuelto un problema matemático de más de cien años de antigüedad.
Forma periódica
En el lenguaje matemático, la teselación de un plano significa el recubrimiento del plano euclidiano con formas poligonales, en donde se da un número finito de formas diferentes. Se llama teselación, por tanto, al patrón que se sigue al recubrir una superficie.
La cuestión es cómo recubrir completamente el plano, sin huecos ni solapamientos, utilizando solamente estas formas y no otras. Lo que ha descubierto esta investigación es que si se usan pentágonos, sólo hay 15 modelos posibles para cubrir el plano.
Por lo general, los azulejos pavimentan un piso de forma periódica, es decir, repitiendo la pavimentación hasta el infinito.
La mayor parte de las técnicas utilizadas en esta investigación pueden ser utilizadas en el caso de polígonos no convexos y podrían servir de base para la solución de otro problema no resuelto en el campo de los pavimentos, conocido como “Einstein Problem”, del alemán “ein stein” (no tiene nada que ver con Albert Einstein), que pretende aclarar si puede existir una baldosa que forme un pavimento no periódico de un plano.
En el lenguaje matemático, la teselación de un plano significa el recubrimiento del plano euclidiano con formas poligonales, en donde se da un número finito de formas diferentes. Se llama teselación, por tanto, al patrón que se sigue al recubrir una superficie.
La cuestión es cómo recubrir completamente el plano, sin huecos ni solapamientos, utilizando solamente estas formas y no otras. Lo que ha descubierto esta investigación es que si se usan pentágonos, sólo hay 15 modelos posibles para cubrir el plano.
Por lo general, los azulejos pavimentan un piso de forma periódica, es decir, repitiendo la pavimentación hasta el infinito.
La mayor parte de las técnicas utilizadas en esta investigación pueden ser utilizadas en el caso de polígonos no convexos y podrían servir de base para la solución de otro problema no resuelto en el campo de los pavimentos, conocido como “Einstein Problem”, del alemán “ein stein” (no tiene nada que ver con Albert Einstein), que pretende aclarar si puede existir una baldosa que forme un pavimento no periódico de un plano.

 Tendencias Científicas
Tendencias Científicas


 Los electrones abren un nuevo mundo a la física cuántica
Los electrones abren un nuevo mundo a la física cuántica CIENCIA ON LINE
CIENCIA ON LINE