En la naturaleza hay multitud de ejemplos de comportamientos ‘inteligentes’, incluso en estructuras sin cerebro, como las células. Aunque la causa de este “conocimiento” natural no ha podido ser explicada por ahora, en las últimas décadas, un lenguaje científico específico ha comenzado a describirlo: el intrincado lenguaje de las matemáticas.
En lo que respecta a las células, resulta difícil creer que estas sigan un comportamiento regido por leyes matemáticas cuando se alimentan, por ejemplo. Sin embargo, según un estudio reciente realizado por investigadores del Instituto de Ciencias Básicas (IBS) de Corea, así es.
Los científicos descubrieron, en concreto, que los orgánulos (endosomas) del interior de las células, cuando portan alimento y lo quieren trasladar a otros orgánulos para su degradación, siguen un tipo de paseo aleatorio (formulación matemática de la trayectoria que resulta de hacer sucesivos pasos aleatorios) llamado vuelo de Lévy.
Esto supone que las células transportan alimento en su interior siguiendo el mismo modelo matemático de movimiento que muchos animales cuando buscan alimento.
Motores intracelulares en vuelo de Lévy
En lenguaje corriente, los endosomas harían lo siguiente: Cuando portan alimento se mueven buscando un objetivo. Lo hacen combinando trayectorias largas y movimientos aleatorios cortos, a lo largo de los microtúbulos o “red de carreteras” intracelular.
Los movimientos cortos son realizados dentro de un área pequeña (entorno inmediato) y los largos, menos frecuentes, son desplegados hacia un área distante. Una vez allí, los orgánulos celulares repiten ambas acciones, hasta encontrar su objetivo (normalmente lisosomas, que son los orgánulos celulares que digieren el material que proviene de fuera de la célula y que penetra en esta por endocitosis).
Según los investigadores coreanos, aunque este patrón de ‘inteligencia inherente’ ya se había estudiado en seres humanos y animales (en medusas, tiburones, aves, y gente), la presente investigación es la primera que identifica un patrón de movimiento semejante en motores moleculares intracelulares.
En lo que respecta a las células, resulta difícil creer que estas sigan un comportamiento regido por leyes matemáticas cuando se alimentan, por ejemplo. Sin embargo, según un estudio reciente realizado por investigadores del Instituto de Ciencias Básicas (IBS) de Corea, así es.
Los científicos descubrieron, en concreto, que los orgánulos (endosomas) del interior de las células, cuando portan alimento y lo quieren trasladar a otros orgánulos para su degradación, siguen un tipo de paseo aleatorio (formulación matemática de la trayectoria que resulta de hacer sucesivos pasos aleatorios) llamado vuelo de Lévy.
Esto supone que las células transportan alimento en su interior siguiendo el mismo modelo matemático de movimiento que muchos animales cuando buscan alimento.
Motores intracelulares en vuelo de Lévy
En lenguaje corriente, los endosomas harían lo siguiente: Cuando portan alimento se mueven buscando un objetivo. Lo hacen combinando trayectorias largas y movimientos aleatorios cortos, a lo largo de los microtúbulos o “red de carreteras” intracelular.
Los movimientos cortos son realizados dentro de un área pequeña (entorno inmediato) y los largos, menos frecuentes, son desplegados hacia un área distante. Una vez allí, los orgánulos celulares repiten ambas acciones, hasta encontrar su objetivo (normalmente lisosomas, que son los orgánulos celulares que digieren el material que proviene de fuera de la célula y que penetra en esta por endocitosis).
Según los investigadores coreanos, aunque este patrón de ‘inteligencia inherente’ ya se había estudiado en seres humanos y animales (en medusas, tiburones, aves, y gente), la presente investigación es la primera que identifica un patrón de movimiento semejante en motores moleculares intracelulares.
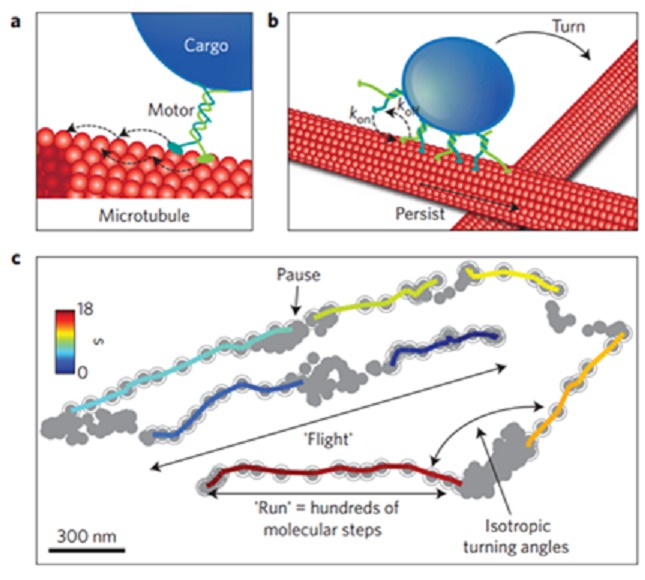
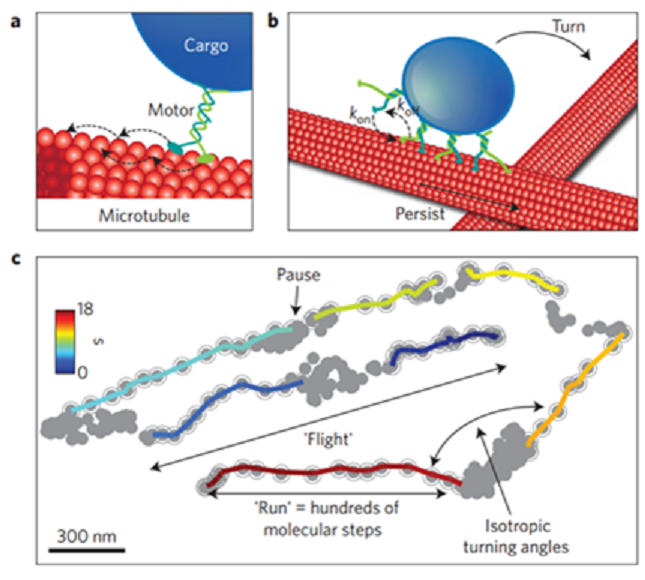
Trayectorias inteligentes de los endosomas dentro de células vivas. Imagen: Nature. Fuente: Alphagalileo.
Hormigas que saben matemáticas
Todavía en el terreno de lo minúsculo, aunque ya desde un punto de vista macroscópico, las hormigas también parecen seguir patrones matemáticos.
Esto último lo ha descubierto un equipo de investigadores de España y EEUU al analizar los movimientos de una clase de hormiga argentina (la Linepithema humile ) al forrajear (buscar alimento) o explorar un territorio vacío (una placa Petri), informa la plataforma Sinc.
En este caso, lo que se ha constatado es que los cambios aleatorios en la dirección de los insectos durante estos procesos siguen unos patrones matemáticos, en concreto, una combinación de distribuciones gaussianas y de Pareto ; dos funciones de probabilidad muy usadas en estadística que en este caso señalan cuanto ‘gira’ la hormiga y hacia dónde en sus desplazamientos.
Aplicaciones bioinspiradas
Más allá de la curiosidad que despiertan, estas investigaciones resultan de gran interés para ciertas aplicaciones. Los científicos coreanos señalan que el patrón matemático encontrado en los orgánulos celulares “resulta prometedor para el diseño de nuevos tipos de materiales activos artificiales".
Los investigadores del segundo estudio afirman, por su parte, que el conocimiento adquirido podría aplicarse en el diseño de grupos de pequeños robots capaces de trabajar de manera coordinada.
En este punto entraríamos en el fascinante terreno de la boinspiración o fabricación de mecanismos inspirados en la biología. De hecho, el traslado de las matemáticas biológicas al campo de los algoritmos ha permitido ya desarrollar enjambres de robots que funcionan como termitas, autoorganizándose y trabajando en equipo sin recibir órdenes.
Todavía en el terreno de lo minúsculo, aunque ya desde un punto de vista macroscópico, las hormigas también parecen seguir patrones matemáticos.
Esto último lo ha descubierto un equipo de investigadores de España y EEUU al analizar los movimientos de una clase de hormiga argentina (la Linepithema humile ) al forrajear (buscar alimento) o explorar un territorio vacío (una placa Petri), informa la plataforma Sinc.
En este caso, lo que se ha constatado es que los cambios aleatorios en la dirección de los insectos durante estos procesos siguen unos patrones matemáticos, en concreto, una combinación de distribuciones gaussianas y de Pareto ; dos funciones de probabilidad muy usadas en estadística que en este caso señalan cuanto ‘gira’ la hormiga y hacia dónde en sus desplazamientos.
Aplicaciones bioinspiradas
Más allá de la curiosidad que despiertan, estas investigaciones resultan de gran interés para ciertas aplicaciones. Los científicos coreanos señalan que el patrón matemático encontrado en los orgánulos celulares “resulta prometedor para el diseño de nuevos tipos de materiales activos artificiales".
Los investigadores del segundo estudio afirman, por su parte, que el conocimiento adquirido podría aplicarse en el diseño de grupos de pequeños robots capaces de trabajar de manera coordinada.
En este punto entraríamos en el fascinante terreno de la boinspiración o fabricación de mecanismos inspirados en la biología. De hecho, el traslado de las matemáticas biológicas al campo de los algoritmos ha permitido ya desarrollar enjambres de robots que funcionan como termitas, autoorganizándose y trabajando en equipo sin recibir órdenes.
Referencias bibliográficas:
Kejia Chen, BoWang y Steve Granick. Memoryless self-reinforcing directionality in endosomal active transport within living cells, Nature Materials (2015). DOI: 10.1038/nmat4239.
M. Vela-Pérez, M. A. Fontelos, S. Garnier. From individual to collective dynamics in Argentine ants (Linepithema humile). Mathematical Biosciences (2015). DOI: 10.1016/j.mbs.2015.01.007.
Marco A. Fontelos, Avner Friedman. A PDE model for the dynamics of trail formation by ants. Journal of Mathematical Analysis and Applications (2015). DOI: 10.1016/j.jmaa.2014.12.030.
Kejia Chen, BoWang y Steve Granick. Memoryless self-reinforcing directionality in endosomal active transport within living cells, Nature Materials (2015). DOI: 10.1038/nmat4239.
M. Vela-Pérez, M. A. Fontelos, S. Garnier. From individual to collective dynamics in Argentine ants (Linepithema humile). Mathematical Biosciences (2015). DOI: 10.1016/j.mbs.2015.01.007.
Marco A. Fontelos, Avner Friedman. A PDE model for the dynamics of trail formation by ants. Journal of Mathematical Analysis and Applications (2015). DOI: 10.1016/j.jmaa.2014.12.030.

 Tendencias Científicas
Tendencias Científicas



 Los electrones abren un nuevo mundo a la física cuántica
Los electrones abren un nuevo mundo a la física cuántica CIENCIA ON LINE
CIENCIA ON LINE