Con motivo del centenario de su nacimiento, en enero de 2012 la prestigiosa revista Nature calificó a Alan Turing como “one of the top scientific minds of all time”. No es difícil estar de acuerdo con esta afirmación.
En 1954, cuando Turing murió, los ordenadores estaban todavía en su tierna infancia. Sus contribuciones fueron prácticamente olvidadas durante casi 20 años, en parte por su homosexualidad, por lo que fue injustamente condenado lo cual le condujo al suicidio, y en parte también por el secreto que rodeó su trabajo en Bletchley Park.
A finales de los años 70, poco después de que la homosexualidad dejara de ser un crimen en el Reino Unido, y después de que se desclasificaran las actividades de Bletchley Park, el legado de Turing empezó a ser reconocido. Además de sus extraordinarias capacidades para descifrar mensajes, Turing es considerado uno de los “padres” de la Informática.
En 1936, es decir, mucho antes de que se construyeran los primeros ordenadores electrónicos, desarrolló los fundamentos teóricos de la computación.
Además, Turing es considerado también el “padre” de la Inteligencia Artificial (IA). En un artículo publicado en 1950, Turing argumentaba que en un plazo de unos 50 años habría ordenadores inteligentes capaces de llevar a cabo deducciones lógicas, de aprender adquiriendo nuevos conocimientos, tanto inductivamente como por experiencia y evolución, y capaces de comunicar mediante interfaces humanizadas. Esta idea era muy radical en aquel momento y de hecho es un debate que todavía persiste.
Por si fuera poco, además de estas fundamentales contribuciones a la computación y a la IA, Turing formuló hace 60 años una teoría sobre la morfogénesis para explicar como se generan los patrones biológicos que dan lugar, por ejemplo, a las rayas en los tigres o las manchas en los leopardos.
En este artículo intentaré dar algunos detalles de estas tres impresionantes contribuciones de Turing. Empecemos pues por su contribución a los fundamentos teóricos de la computación.
Conceptos teóricos de los ordenadores
A la edad de 24 años, Turing, publicó en la revista “Proceedings of the London Mathematical Society” los conceptos teóricos sobre los que se basan todos los ordenadores actuales. En efecto, la máquina de Turing es una rigurosa formalización de conceptos tan básicos en informática como el concepto de algoritmo y el concepto de calculabilidad y gracias a estos conceptos determinó donde están los límites de lo que es calculable por un ordenador.
Demostrar imposibilidades es de importancia extraordinaria en ciencia. Por ejemplo, la imposibilidad de construir máquinas con movimiento perpetuo condujo al descubrimiento de las leyes de la termodinámica en física.
De la misma forma, conocer los límites de las matemáticas y de la computación nos puede enseñar algunas reglas básicas acerca de sus posibilidades o, como muy bien dice el matemático Gregory Chaitin, nos permite saber cuándo no debemos intentar lo imposible.
Turing, de hecho, no pretendía inventar un modelo teórico de los ordenadores modernos. Lo que quería era resolver un problema en lógica matemática llamado “Entscheidungsproblem” o problema de la decisión, formulado en 1928 por David Hilbert.
Por aquel entonces los matemáticos estaban investigando sobre los fundamentos de la matemática y Hilbert planteó la pregunta de si todo enunciado matemático (como por ejemplo “2+2=4”) era decidible o no.
En otras palabras, ¿existe un procedimiento mecánico paso a paso tal que dado cualquier enunciado matemático permita determinar si éste es cierto o falso?
Bien que la respuesta es obvia para el enunciado “2+2=4”, sabemos que hay muchos enunciados cuya respuesta requiere esfuerzos extraordinarios (por ejemplo el último teorema de Fermat) y muchos otros que todavía no tienen respuesta como por ejemplo la conjetura de Riemann, que tiene que ver con la distribución de los números primos, que data de 1859 y, aunque todo el mundo sospecha que es cierta, todavía no se ha podido demostrar.
Incluso el propio Turing dedicó grandes esfuerzos en intentar demostrarla y estaba convencido que los ordenadores jugarían un papel importante en su demostración.
Procedimiento paso a paso
Si existiera un procedimiento tal que, dado un enunciado matemático, permitiera determinar si éste es cierto o falso, entonces todas las grandes cuestiones de las matemáticas podrían ser resueltas. Hilbert confiaba en que dicho procedimiento existiera.
De hecho lo que él llamaba “procedimiento mecánico pasa a paso” hoy día lo llamamos “algoritmo” y por lo tanto lo que Hilbert buscaba era de hecho un programa de ordenador. Turing así lo intuyó y para poder intentar responder a la pregunta de Hilbert, tuvo que definir previamente que es un “procedimiento pasa a paso” y que tipo de dispositivo lo podría llevar a cabo. No se trataba de construir materialmente dicho dispositivo, sino de especificar claramente su funcionamiento.
Inicialmente especificó una máquina capaz de leer y escribir sobre una cinta de papel (que puede ser infinita). El cabezal lector/escritor de la máquina en cada paso lee un símbolo contenido en la cinta y en función del valor de este símbolo y de su estado interno toma una decisión acerca de qué acción hacer a continuación siguiendo un conjunto de reglas internas.
El repertorio de acciones es muy sencillo: desplazar la cinta hacia la izquierda o hacia la derecha, borrar el símbolo leído, escribir un símbolo, o parar. Esta máquina es lo que conocemos ahora cómo “Máquina de Turing”.
El problema era que al tener un conjunto fijo y predefinido de reglas internas no servía para dar respuesta a la pregunta de Hilbert sobre la decidibilidad.
La genialidad de Turing le permitió darse cuenta que era posible usar la propia cinta para introducir en la máquina el conjunto de reglas internas que determinaran su funcionamiento. Gracias a ello, la máquina se convertía en programable y por consiguiente podía simular cualquier otra máquina con reglas fijas. Esta nueva máquina, que actualmente llamamos “Máquina Universal de Turing”, no es otra cosa que un ordenador.
Ahora ya sí, Turing tenía su ordenador teórico con el cual poder responder a la pregunta: ¿qué es calculable?. Es decir ¿que es lo que puede y no puede hacer un ordenador?. Para responder la pregunta de Hilbert, Turing buscaba un contraejemplo, es decir una expresión concreta de forma que la máquina no pudiera determinar ni su certeza ni su falsedad.
La cuestión que permitió a Turing resolver el problema es: ¿Puede una máquina examinar cualquier programa y decidir si se detendrá, dando una respuesta, o bien nunca se detendrá?. En otras palabras, ¿puede un ordenador determinar si es cierto o falso que cualquier programa se detendrá? Turing demostró que la respuesta a esta pregunta es NO y por consiguiente el procedimiento mecánico paso a paso deseado por Hilbert no existe y el Entscheidungsproblem de Hilbert quedó resuelto.
Turing no había únicamente logrado resolver el problema de la decisión formulado por Hilbert sino que, de paso y sin realmente pretenderlo, había establecido los fundamentos teóricos de la computación.
A la edad de 24 años, Turing, publicó en la revista “Proceedings of the London Mathematical Society” los conceptos teóricos sobre los que se basan todos los ordenadores actuales. En efecto, la máquina de Turing es una rigurosa formalización de conceptos tan básicos en informática como el concepto de algoritmo y el concepto de calculabilidad y gracias a estos conceptos determinó donde están los límites de lo que es calculable por un ordenador.
Demostrar imposibilidades es de importancia extraordinaria en ciencia. Por ejemplo, la imposibilidad de construir máquinas con movimiento perpetuo condujo al descubrimiento de las leyes de la termodinámica en física.
De la misma forma, conocer los límites de las matemáticas y de la computación nos puede enseñar algunas reglas básicas acerca de sus posibilidades o, como muy bien dice el matemático Gregory Chaitin, nos permite saber cuándo no debemos intentar lo imposible.
Turing, de hecho, no pretendía inventar un modelo teórico de los ordenadores modernos. Lo que quería era resolver un problema en lógica matemática llamado “Entscheidungsproblem” o problema de la decisión, formulado en 1928 por David Hilbert.
Por aquel entonces los matemáticos estaban investigando sobre los fundamentos de la matemática y Hilbert planteó la pregunta de si todo enunciado matemático (como por ejemplo “2+2=4”) era decidible o no.
En otras palabras, ¿existe un procedimiento mecánico paso a paso tal que dado cualquier enunciado matemático permita determinar si éste es cierto o falso?
Bien que la respuesta es obvia para el enunciado “2+2=4”, sabemos que hay muchos enunciados cuya respuesta requiere esfuerzos extraordinarios (por ejemplo el último teorema de Fermat) y muchos otros que todavía no tienen respuesta como por ejemplo la conjetura de Riemann, que tiene que ver con la distribución de los números primos, que data de 1859 y, aunque todo el mundo sospecha que es cierta, todavía no se ha podido demostrar.
Incluso el propio Turing dedicó grandes esfuerzos en intentar demostrarla y estaba convencido que los ordenadores jugarían un papel importante en su demostración.
Procedimiento paso a paso
Si existiera un procedimiento tal que, dado un enunciado matemático, permitiera determinar si éste es cierto o falso, entonces todas las grandes cuestiones de las matemáticas podrían ser resueltas. Hilbert confiaba en que dicho procedimiento existiera.
De hecho lo que él llamaba “procedimiento mecánico pasa a paso” hoy día lo llamamos “algoritmo” y por lo tanto lo que Hilbert buscaba era de hecho un programa de ordenador. Turing así lo intuyó y para poder intentar responder a la pregunta de Hilbert, tuvo que definir previamente que es un “procedimiento pasa a paso” y que tipo de dispositivo lo podría llevar a cabo. No se trataba de construir materialmente dicho dispositivo, sino de especificar claramente su funcionamiento.
Inicialmente especificó una máquina capaz de leer y escribir sobre una cinta de papel (que puede ser infinita). El cabezal lector/escritor de la máquina en cada paso lee un símbolo contenido en la cinta y en función del valor de este símbolo y de su estado interno toma una decisión acerca de qué acción hacer a continuación siguiendo un conjunto de reglas internas.
El repertorio de acciones es muy sencillo: desplazar la cinta hacia la izquierda o hacia la derecha, borrar el símbolo leído, escribir un símbolo, o parar. Esta máquina es lo que conocemos ahora cómo “Máquina de Turing”.
El problema era que al tener un conjunto fijo y predefinido de reglas internas no servía para dar respuesta a la pregunta de Hilbert sobre la decidibilidad.
La genialidad de Turing le permitió darse cuenta que era posible usar la propia cinta para introducir en la máquina el conjunto de reglas internas que determinaran su funcionamiento. Gracias a ello, la máquina se convertía en programable y por consiguiente podía simular cualquier otra máquina con reglas fijas. Esta nueva máquina, que actualmente llamamos “Máquina Universal de Turing”, no es otra cosa que un ordenador.
Ahora ya sí, Turing tenía su ordenador teórico con el cual poder responder a la pregunta: ¿qué es calculable?. Es decir ¿que es lo que puede y no puede hacer un ordenador?. Para responder la pregunta de Hilbert, Turing buscaba un contraejemplo, es decir una expresión concreta de forma que la máquina no pudiera determinar ni su certeza ni su falsedad.
La cuestión que permitió a Turing resolver el problema es: ¿Puede una máquina examinar cualquier programa y decidir si se detendrá, dando una respuesta, o bien nunca se detendrá?. En otras palabras, ¿puede un ordenador determinar si es cierto o falso que cualquier programa se detendrá? Turing demostró que la respuesta a esta pregunta es NO y por consiguiente el procedimiento mecánico paso a paso deseado por Hilbert no existe y el Entscheidungsproblem de Hilbert quedó resuelto.
Turing no había únicamente logrado resolver el problema de la decisión formulado por Hilbert sino que, de paso y sin realmente pretenderlo, había establecido los fundamentos teóricos de la computación.
Turing y la IA
Turing estaba muy interesado también por el funcionamiento del cerebro. Estaba convencido de que el córtex cerebral de un niño pequeño podía ser simulado mediante un ordenador.
En 1948 escribió un poco conocido artículo sobre ello titulado “Intelligent Machinery” y al hacerlo describió lo que ahora conocemos cómo “redes neuronales artificiales”. Dicho artículo, que de hecho no se publicó hasta 1969, presenta un modelo del cerebro basado en unidades de procesamiento muy sencillas. Estas unidades están conectadas entre sí de forma aleatoria formando una red. La señales que procesan son binarias por lo que actualmente estas redes las llamaríamos “redes booleanas”. Turing las llamó “máquinas no-organizadas de tipo A” y la salida de cada unidad se calcula mediante el producto de los valores binarios de las entradas restado de 1, es decir que de hecho cada unidad es una puerta lógica de tipo NAND.
Estas máquinas de tipo A no podían aprender, por lo que Turing las extendió añadiendo una especie de interruptores en las conexiones entre las neuronas que podían ser entrenados por un agente externo que le enseña a resolver una tarea dada. Turing las llamó “máquinas de tipo B”. El entrenamiento de la red consistiría en bloquear o desbloquear la conexión entre neuronas mediante el interruptor hasta llegar a una máquina “organizada” convenientemente, para llevar a cabo la tarea para la que ha sido entrenada.
Sin embargo, Turing no propuso ningún algoritmo que realizara dicho entrenamiento. Poco después de su muerte se pudo demostrar que estas redes neuronales booleanas son efectivamente entrenables para, por ejemplo, aprender a discriminar entre clases linealmente separables.
Actualmente, redes neuronales artificiales, organizadas por capas, más complejas que las propuestas por Turing se usan extensivamente en IA y Robótica. En su artículo de 1948 Turing también describe unas máquinas que él llama “de tipo P” entrenables mediante un proceso de “premio o castigo”, es decir que de nuevo Turing anticipó lo que actualmente se conoce como “aprendizaje por refuerzo” y que es una de las técnicas de aprendizaje más exitosas en IA.
Las máquinas de tipo P, contrariamente a las de tipo A y B, no eran redes neuronales binarias, sino máquinas de Turing modificadas de forma que, antes de ser entrenadas, el conjunto de sus reglas internas es incompleto pero después de ser entrenadas se llega a un conjunto completo de reglas.
Test de Turing
En el contexto de estos trabajos sobre máquinas inteligentes, Turing no podía pasar por alto la cuestión de cómo averiguar si una máquina es o no inteligente y, con el fin de responder a esta pregunta, propuso el test que lleva su nombre en un artículo publicado en la revista Mind en 1950 titulado “Computing Machinery and Intelligence”.
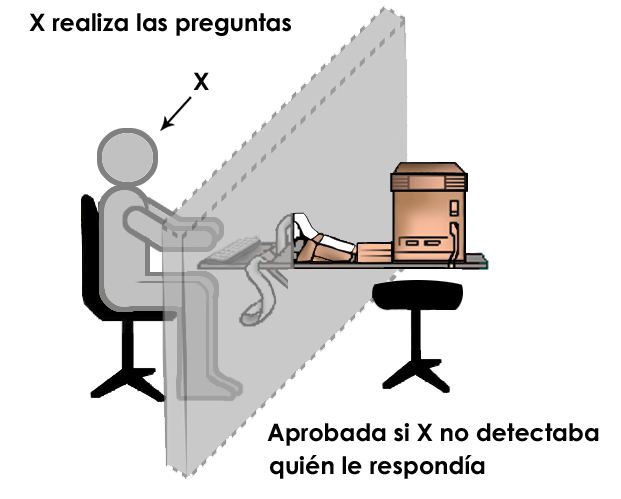
El test de Turing es una variante del llamado “juego de imitación” en el que en su versión original participaban tres personas, un interrogador, un hombre y una mujer. El interrogador se sitúa en una sala distinta y se comunica con las otras dos personas mediante mensajes de texto usando un terminal de ordenador y dispone de cinco minutos para, a través de las respuestas que recibe a sus preguntas, determinar con suficiente certeza quien es el hombre y quien la mujer.
Esto sería fácil sino fuera porque en este juego el hombre miente, pretendiendo ser la mujer con el objetivo de confundir al interrogador. La mujer por su parte intenta, a través de sus respuestas, ayudar al interrogador a discernir correctamente quien es quien. Si pasados los cinco minutos el interrogador no es capaz de saber con una certeza superior al 70% quien es quien, entonces el hombre gana el juego ya que ha conseguido confundir al interrogador haciéndose pasar por mujer.
Pues bien, el test de Turing consiste simplemente en substituir en este juego de imitación el papel del hombre por un ordenador. De tal forma que si consigue confundir al interrogador, haciéndole creer que es la una persona, diremos que el ordenador es inteligente.
Si bien es cierto que hasta ahora no hay ningún programa de ordenador que haya superado este test, hay que decir que tampoco es realmente un objetivo de los investigadores en IA conseguir superarlo y por lo tanto no se han dedicado muchos esfuerzos a ello, exceptuando los diálogos completamente intranscendentes del muy criticado “Premio Loebner”.
Turing estaba muy interesado también por el funcionamiento del cerebro. Estaba convencido de que el córtex cerebral de un niño pequeño podía ser simulado mediante un ordenador.
En 1948 escribió un poco conocido artículo sobre ello titulado “Intelligent Machinery” y al hacerlo describió lo que ahora conocemos cómo “redes neuronales artificiales”. Dicho artículo, que de hecho no se publicó hasta 1969, presenta un modelo del cerebro basado en unidades de procesamiento muy sencillas. Estas unidades están conectadas entre sí de forma aleatoria formando una red. La señales que procesan son binarias por lo que actualmente estas redes las llamaríamos “redes booleanas”. Turing las llamó “máquinas no-organizadas de tipo A” y la salida de cada unidad se calcula mediante el producto de los valores binarios de las entradas restado de 1, es decir que de hecho cada unidad es una puerta lógica de tipo NAND.
Estas máquinas de tipo A no podían aprender, por lo que Turing las extendió añadiendo una especie de interruptores en las conexiones entre las neuronas que podían ser entrenados por un agente externo que le enseña a resolver una tarea dada. Turing las llamó “máquinas de tipo B”. El entrenamiento de la red consistiría en bloquear o desbloquear la conexión entre neuronas mediante el interruptor hasta llegar a una máquina “organizada” convenientemente, para llevar a cabo la tarea para la que ha sido entrenada.
Sin embargo, Turing no propuso ningún algoritmo que realizara dicho entrenamiento. Poco después de su muerte se pudo demostrar que estas redes neuronales booleanas son efectivamente entrenables para, por ejemplo, aprender a discriminar entre clases linealmente separables.
Actualmente, redes neuronales artificiales, organizadas por capas, más complejas que las propuestas por Turing se usan extensivamente en IA y Robótica. En su artículo de 1948 Turing también describe unas máquinas que él llama “de tipo P” entrenables mediante un proceso de “premio o castigo”, es decir que de nuevo Turing anticipó lo que actualmente se conoce como “aprendizaje por refuerzo” y que es una de las técnicas de aprendizaje más exitosas en IA.
Las máquinas de tipo P, contrariamente a las de tipo A y B, no eran redes neuronales binarias, sino máquinas de Turing modificadas de forma que, antes de ser entrenadas, el conjunto de sus reglas internas es incompleto pero después de ser entrenadas se llega a un conjunto completo de reglas.
Test de Turing
En el contexto de estos trabajos sobre máquinas inteligentes, Turing no podía pasar por alto la cuestión de cómo averiguar si una máquina es o no inteligente y, con el fin de responder a esta pregunta, propuso el test que lleva su nombre en un artículo publicado en la revista Mind en 1950 titulado “Computing Machinery and Intelligence”.
El test de Turing es una variante del llamado “juego de imitación” en el que en su versión original participaban tres personas, un interrogador, un hombre y una mujer. El interrogador se sitúa en una sala distinta y se comunica con las otras dos personas mediante mensajes de texto usando un terminal de ordenador y dispone de cinco minutos para, a través de las respuestas que recibe a sus preguntas, determinar con suficiente certeza quien es el hombre y quien la mujer.
Esto sería fácil sino fuera porque en este juego el hombre miente, pretendiendo ser la mujer con el objetivo de confundir al interrogador. La mujer por su parte intenta, a través de sus respuestas, ayudar al interrogador a discernir correctamente quien es quien. Si pasados los cinco minutos el interrogador no es capaz de saber con una certeza superior al 70% quien es quien, entonces el hombre gana el juego ya que ha conseguido confundir al interrogador haciéndose pasar por mujer.
Pues bien, el test de Turing consiste simplemente en substituir en este juego de imitación el papel del hombre por un ordenador. De tal forma que si consigue confundir al interrogador, haciéndole creer que es la una persona, diremos que el ordenador es inteligente.
Si bien es cierto que hasta ahora no hay ningún programa de ordenador que haya superado este test, hay que decir que tampoco es realmente un objetivo de los investigadores en IA conseguir superarlo y por lo tanto no se han dedicado muchos esfuerzos a ello, exceptuando los diálogos completamente intranscendentes del muy criticado “Premio Loebner”.
Robots autónomos
El principal motivo de porque no es un objetivo en IA es que, en base al estado actual de la IA, este juego de imitación no es un buen indicador para determinar si una máquina es inteligente ya que, como mucho, solamente evalúa aquellos procesos cognitivos que son susceptibles de ser expresados verbalmente.
Sin embargo hay otros procesos cognitivos fundamentales que no son verbalizables y cuya modelización y evaluación son imprescindibles en IA.
El ejemplo más paradigmático es la actual investigación en robots autónomos, cuyo objetivo es dotarles de sofisticadas habilidades sensoriales y motoras, que permitirán que dichos robots puedan aprender a reconocer y comprender lo que vean, toquen, oigan y huelan.
También deberán tener capacidades de razonamiento espacial para aprender a interpretar su entorno que generalmente incluirá a otros robots y también a seres humanos, lo que requerirá que también desarrollen capacidades de socialización.
Para poder medir los progresos hacia estos objetivos, un test como el propuesto por Turing no sirve. Necesitamos más bien un conjunto de tests que evalúen todo el rango de capacidades que conforman la inteligencia, y en particular la capacidad de adquirir conocimientos de sentido común, el problema más importante que debemos resolver para conseguir inteligencias artificiales de propósito general.
En cualquier caso, la repercusión más importante del Test de Turing es de carácter filosófico, ya que dicho test implica que para decidir si una máquina es inteligente lo importante es observar externamente si tiene o no un comportamiento inteligente, en lugar de analizar cómo sus estructuras y mecanismos causales internos dan lugar a inteligencia.
Actualmente esta es una cuestión que genera mucha polémica entre filósofos de la mente como por ejemplo la existente entre John Searle y Paul y Patricia Churchland.
Turing y la Biología del desarrollo
La última, y asombrosa, noticia sobre la genialidad de Turing es del pasado 2012. Investigadores del King’s College de Londres han confirmado experimentalmente una teoría que Turing formuló, hace algo más de 60 años, que explicaba como se generan los patrones biológicos que, durante el desarrollo embrionario, dan lugar, por ejemplo, a las rayas en los tigres o las manchas en los leopardos.
El estudio, publicado en la prestigiosa revista Nature Genetics, demuestra que dichos patrones se deben a la interacción de un par de morfogenes, uno “inhibidor” y otro “activador”, tal y como predecían las ecuaciones no lineales de reacción-difusión que había formulado Turing en un artículo publicado en 1952 en Philosophical Transactions of the Royal Society of London.
Turing estaba interesado en explicar como un conjunto inicialmente homogéneo de células embrionarias puede dar lugar a patrones no homogéneos tan complejos y variados.
Turing encontró que si en estas ecuaciones de reacción-difusión (que modelizan las interacciones entre el morfogen activador y el morfogen inhibidor), la velocidad de producción del morfogen inhibidor es mayor que la velocidad de producción del morfogen activador, entonces se rompe el equilibrio inestable inicial del sistema y se generan los patrones.
Estas roturas del equilibrio son debidas a perturbaciones que se cree son debidas a variaciones estadísticas en las velocidades de producción y de difusión de los morfogenes.
Este resultado es de tal magnitud que puede incluso tener aplicaciones importantes en medicina regenerativa.
A la vista de tantas y tan variadas contribuciones científicas al más alto nivel, a nadie se le escapa pensar cuantas veces más nos hubiera asombrado Alan Turing con otras contribuciones científicas de primer orden si la intolerancia no se hubiera cruzado en su camino.
(*) Ramón López de Mántaras es el Director del Instituto de Investigación en Inteligencia Artificial (IIIA), perteneciente al Consejo Superior de Investigaciones Científicas.
El principal motivo de porque no es un objetivo en IA es que, en base al estado actual de la IA, este juego de imitación no es un buen indicador para determinar si una máquina es inteligente ya que, como mucho, solamente evalúa aquellos procesos cognitivos que son susceptibles de ser expresados verbalmente.
Sin embargo hay otros procesos cognitivos fundamentales que no son verbalizables y cuya modelización y evaluación son imprescindibles en IA.
El ejemplo más paradigmático es la actual investigación en robots autónomos, cuyo objetivo es dotarles de sofisticadas habilidades sensoriales y motoras, que permitirán que dichos robots puedan aprender a reconocer y comprender lo que vean, toquen, oigan y huelan.
También deberán tener capacidades de razonamiento espacial para aprender a interpretar su entorno que generalmente incluirá a otros robots y también a seres humanos, lo que requerirá que también desarrollen capacidades de socialización.
Para poder medir los progresos hacia estos objetivos, un test como el propuesto por Turing no sirve. Necesitamos más bien un conjunto de tests que evalúen todo el rango de capacidades que conforman la inteligencia, y en particular la capacidad de adquirir conocimientos de sentido común, el problema más importante que debemos resolver para conseguir inteligencias artificiales de propósito general.
En cualquier caso, la repercusión más importante del Test de Turing es de carácter filosófico, ya que dicho test implica que para decidir si una máquina es inteligente lo importante es observar externamente si tiene o no un comportamiento inteligente, en lugar de analizar cómo sus estructuras y mecanismos causales internos dan lugar a inteligencia.
Actualmente esta es una cuestión que genera mucha polémica entre filósofos de la mente como por ejemplo la existente entre John Searle y Paul y Patricia Churchland.
Turing y la Biología del desarrollo
La última, y asombrosa, noticia sobre la genialidad de Turing es del pasado 2012. Investigadores del King’s College de Londres han confirmado experimentalmente una teoría que Turing formuló, hace algo más de 60 años, que explicaba como se generan los patrones biológicos que, durante el desarrollo embrionario, dan lugar, por ejemplo, a las rayas en los tigres o las manchas en los leopardos.
El estudio, publicado en la prestigiosa revista Nature Genetics, demuestra que dichos patrones se deben a la interacción de un par de morfogenes, uno “inhibidor” y otro “activador”, tal y como predecían las ecuaciones no lineales de reacción-difusión que había formulado Turing en un artículo publicado en 1952 en Philosophical Transactions of the Royal Society of London.
Turing estaba interesado en explicar como un conjunto inicialmente homogéneo de células embrionarias puede dar lugar a patrones no homogéneos tan complejos y variados.
Turing encontró que si en estas ecuaciones de reacción-difusión (que modelizan las interacciones entre el morfogen activador y el morfogen inhibidor), la velocidad de producción del morfogen inhibidor es mayor que la velocidad de producción del morfogen activador, entonces se rompe el equilibrio inestable inicial del sistema y se generan los patrones.
Estas roturas del equilibrio son debidas a perturbaciones que se cree son debidas a variaciones estadísticas en las velocidades de producción y de difusión de los morfogenes.
Este resultado es de tal magnitud que puede incluso tener aplicaciones importantes en medicina regenerativa.
A la vista de tantas y tan variadas contribuciones científicas al más alto nivel, a nadie se le escapa pensar cuantas veces más nos hubiera asombrado Alan Turing con otras contribuciones científicas de primer orden si la intolerancia no se hubiera cruzado en su camino.
(*) Ramón López de Mántaras es el Director del Instituto de Investigación en Inteligencia Artificial (IIIA), perteneciente al Consejo Superior de Investigaciones Científicas.

 Tendencias Científicas
Tendencias Científicas





 Las neuronas de un compositor siguen creando música 4 años después de su muerte
Las neuronas de un compositor siguen creando música 4 años después de su muerte CIENCIA ON LINE
CIENCIA ON LINE