|
|
Blog de Tendencias21 sobre materia, energía, dinámicas y procesos
Continuamos con el estudio de Arturo Rodriguez sobre el llamado bamboleo de Chandler, que le ocurre a nuestro planeta Tierra. La pequeña variación en la posición del eje de rotación de la Tierra detectad por Chandler, según expresa este investigador, puede explicarse más fácilmente a partir de la Teoría de Interacciones Dinámicas. Seguimos reproduciendo su análisis:
El experimento de laboratorio representado en la figura 2, está descrito en el documento A: A Lab for Exploring the Precession and Nutation of a Gyroscope, que puede encontrarse fácilmente en Internet. Además, disponemos de los datos obtenidos en el laboratorio y que nos fueron suministrados por el autor del mismo. Gracias a estos datos hemos podido contrastar nuestras ideas con la realidad observada. Los datos teóricos de han obtenido mediante la simulación por ordenador (en lenguaje Maple) de la aproximación lagrangiana del problema, tal como está descrito en el documento B: “Physics with Maple The Computer Algebra Resource for Mathematical Methods in Physics ed. 2005” que utilizó el autor del experimento para obtener la función lagrangiana:

donde q1 = ϕ, q2 = θ, q3 = ψ son los ángulos de Euler.
En nuestro estudio, vamos a analizar particularmente el caso f descrito en el documento A:

En esta gráfica podemos observar el amortiguamiento del valor de la velocidad angular de nutación (dθ/dt) hasta un valor constante indicado en la figura por Δθ. El autor del experimento achaca este fenómeno a la acción rozamiento del giróscopo con la pieza de apoyo o cojinete que lo sujeta, que se podría simular en el programa introduciendo en las ecuaciones de la dinámica un término proporcional a la derivada de la componente de la velocidad angular correspondiente a la nutación.
Sin embargo, la fricción es un proceso físico no conservativo y, por tanto, debería afectar al movimiento de rotación en su conjunto y no solamente a una de sus componentes, ya que en ese caso se manifestaría un comportamiento selectivo que no se puede justificar. Sin embargo, en nuestro modelo, esta amortiguación se produce de forma natural, sin contradecir principios como la segunda ley de la termodinámica; recordemos que las fuerzas conservativas aumentan la entropía del sistema, lo cual se contradice con la supresión selectiva del movimiento de nutación, debido a que ésta supondría un mayor orden estructural en lo que a la dinámica del cuerpo se refiere.
Para llegar a esto fue necesario realizar modificaciones en el modelo teórico convencional, tal como fue simulado originalmente y que da lugar a la curva en azul de la gráfica de la figura 3. La curva en rojo corresponde al valor obtenido experimentalmente en el laboratorio. Pues bien, en nuestra gráfica de la figura 4 presentamos en color rojo la curva correspondiente al valor predicho por nuestra teoría y mantenemos el color azul para visualizar la curva obtenida por el método convencionalmente aceptado, que ya hemos descrito anteriormente.

Es un hecho probado la poca incidencia que tiene el movimiento de nutación en este tipo de fenómenos, en los cuales pasa casi desapercibido. En nuestro modelo este amortiguamiento se puede justificar sin necesidad de añadir hipótesis, como es la posibilidad de que esto sea debido al rozamiento que afectaría a la nutación de forma selectiva, como hemos comentado anteriormente. Sería interesante realizar experimentos en vacío que corroboren lo que postulamos aquí.
Antes de desarrollar las ecuaciones de nuestra teoría, es conveniente recordar los conceptos de la física actual con los que, de forma comúnmente aceptada, se analiza el problema en cuestión. Por una parte, tenemos las ecuaciones de Euler para la dinámica rotacional del sólido rígido que, aparentemente se derivan de la conservación del momento angular total del cuerpo, sumando de forma arbitraria la acción de pares de fuerza no coaxiales. En nuestra teoría, el momento angular está disociado en dos vectores independientes, cada uno de ellos está asociado a uno solo de los torques no coaxiales y que forman parte se sistemas de ecuaciones independientes, aunque acoplados a través de otras variables comunes que aparecen en ambos sistemas.
Esto se logra mediante la separación de la parte real y de la parte compleja en las igualdades que aparecen en las ecuaciones del movimiento. Este procedimiento no es el habitual en mecánica clásica, donde solo se consideran valores reales, mientras que los imaginarios se rechazan por “no físicos”.
En la actualidad, la versión relativista de la mecánica postula que las todas las aceleraciones, incluidas las inerciales, son equivalentes a un campo gravitatorio, en lo que se conoce como principio de equivalencia fuerte y que fue postulado por Einstein en su teoría de la relatividad general.
Nosotros coincidimos con los principios d la TID que sostienen que dichas aceleraciones deberían estar fuera del principio de equivalencia, el cual tendría que estar solamente referido a aceleraciones lineales que no generen rotación, dejando así un principio de equivalencia débil más limitado y que permita situar el problema que estamos tratando dentro de un marco más extenso. Desde nuestro punto de vista, dicha extensión se basaría en la posibilidad de incluir funciones y números complejos para modelar la realidad física.
Coincidimos plenamente con lo expresado en el artículo del autor de la TID: ”ON THE EQUIVALENCE PRINCIPLE” en el sentido de que un observador sí que podría distinguir, respecto de un campo gravitatorio, los efectos producidos por pares de fuerzas no coaxiales en un cuerpo por las razones que en dicho artículo se describen.
Como consecuencia, el sacar estos fenómenos fuera del marco del principio de equivalencia, implicaría postular una nueva simetría distinta a la empleada en la relatividad general, que es conocida como el grupo de difeomorfismos y que viene a decir que las ecuaciones de campo de la gravedad son invariantes ante cualquier cambio del sistema de coordenadas definido por el tensor métrico.
Si queremos postular una nueva teoría alternativa a la actualmente aceptada, tendremos que demostrar que dicha teoría está gobernada por cierto grupo de simetría distinto, aún por descubrir y que, por analogía con otros fenómenos físicos sería lógico que fuera una simetría de tipo gauge. En nuestro caso, habría que buscar la invariancia del sistema físico al ser sometido a diversas modificaciones en los valores de las cargas de pares de fuerzas, en lugar de fuerza tal como se suele interpretar. (ver la entrada sobre “simetría de gauge” en Wikipedia). Veremos más adelante que el grupo de simetría de gauge de nuestra teoría es el SO(4)/Z2.
Antes de entrar en detalles sobre el desarrollo matemático de nuestra teoría, procedemos a continuación a resumir brevemente el movimiento de Chandler que experimenta la tierra como consecuencia de su movimiento de rotación-precesión-nutación.
Por un lado, la tierra gira sobre un eje en un movimiento que denominamos rotación intrínseca, causa de que haya días y noches. Desde la antigüedad se sabe también que nuestro planeta experimenta un movimiento llamado “precesión de los equinoccios” y que consiste, básicamente, en el giro del eje de rotación alrededor otro eje, describiendo, por tanto, la trayectoria del eje de rotación intrínseca la superficie de un cono.
Dicha trayectoria puede sufrir a su vez oscilaciones periódicas alrededor de un tercer eje perpendicular a los anteriores, dando lugar al movimiento conocido como nutación. El par que produce estos movimientos consiste en la atracción gravitatoria simultánea del sol y la luna sobre el abultamiento del planeta en el ecuador. También influye la atracción de los planetas.
El conocimiento de la precesión de los equinoccios ha sido muy importante históricamente, especialmente en navegación, ya que dicho movimiento modifica el lugar (se considera, en realidad, la estrella más cercana a ese lugar) al que apunta el eje de rotación. Actualmente, apunta a la estrella polar, pero en tiempos remotos el punto exacto estaba considerablemente desviado de ésta y en el futuro apuntará a otra estrella distinta: Vega. Como sabemos, este movimiento es extraordinariamente lento comparado con el de rotación.
Simultáneamente, todavía existe un segundo movimiento de precesión y nutación experimentado por la tierra, probablemente ya conocido desde la antigüedad, ya que da lugar a variaciones del orden de décimas de segundos de arco, lo cual produce un error no despreciable en cálculos para navegación y que, en principio no se podía justificar mediante torques producidos por la gravedad de newton. Este fenómeno fue aparentemente explicado en principio por Euler en siglo XVIII al considerar que era el resultado de sus famosas ecuaciones del movimiento rotacional del sólido rígido en ausencia de pares fe fuerzas.
A este fenómeno lo denominó precesión y nutación libres, con un periodo de unos diez meses de la variación de la latitud, según sus cálculos. La verificación experimental y análisis de este movimiento se lleva a cabo en el siglo XIX por S.C. Chandler y desde entonces lleva su nombre. El valor del periodo obtenido en sus medidas dio como resultado 428 días, un 40 por ciento mayor del esperado respecto al dado por Euler.
Actualmente, se ha medido con gran precisión un periodo de 436 días y una amplitud aproximadamente de 0,1 segundos de arco. Finalmente, el astrónomo Newcomb achaca esta diferencia a la no rigidez de la tierra y postula la existencia de dos periodos independientes: uno propio de Chandler y otro anual producido por variaciones de masas de la atmósfera.
Sin embargo, lo que nos llama la atención es que, para explicar este fenómeno, se utilice un segundo sistema de ecuaciones de Euler para torques nulos, independiente del necesario para explicar la precesión de los equinoccios para torques producidos por fuerzas gravitacionales procedentes del sol y la luna, ya que se están utilizando dos variables distintas, correspondientes a dos momentos angulares diferentes, aplicados en el mismo objeto. Pero esto va en contra de la propia teoría clásica aceptada, ya que dichos momentos se sumarían vectorialmente.
Actualmente, en mecánica clásica se acepta, en nuestra opinión errónea y arbitrariamente, que los momentos angulares correspondientes a torques aplicados en el cuerpo según ejes no coaxiales se pueden sumar algebraicamente, tal como se hace con otras magnitudes vectoriales, como las fuerzas aplicadas a un cuerpo en el centro de gravedad.
Por eso nos sorprende tanto que, en el problema que estamos tratando sobre el movimiento rotacional de la tierra, no se aplique ese mismo criterio y se postulen dos vectores distintos, por una parte, para el momento angular que produce la precesión inducida por el tirón gravitatorio de objetos celestes cercanos y, por otra, un momento angular diferente asociado a la llamada precesión libre, que daría lugar al movimiento de Chandler y con una de las componentes común a ambos casos correspondiente a la rotación intrínseca.
Quizás para disimular, de alguna manera, esta falta de coherencia teórica, se denomina en la literatura sobre el tema “precesión de los equinoccios” al primer fenómeno y “nutación de Chandler” al segundo, cuando en realidad ambos movimientos presentan al mismo tiempo tanto precesión como nutación de forma simultánea.
Sin embargo, es interesante remarcar que en nuestro modelo sí que es posible tener vectores de momento angular independientes siempre que aparezcan en forma compleja; uno como la parte real y el otro la parte imaginaria. Posteriormente, al elevar al cuadrado las magnitudes correspondientes para obtener la función Lagrangiana del sistema, el numero imaginario desaparece ya que su valor al cuadrado es -1. Así tenemos que, manejando magnitudes complejas, al final solo aparecen números reales en las ecuaciones del movimiento.
ste procedimiento es que llevamos a cabo para proceder a la simulación de nuestra teoría mediante un programa informático en el entorno de programación en lenguaje Maple, que se puede utilizar para resolver en el ordenador sistemas de ecuaciones diferenciales, entre otras muchas utilidades matemáticas.
El modelo físico del sistema que estamos estudiando se puede implementar mediante la llamada aproximación lagrangiana, consistente en partir de una función de las coordenadas y las velocidades que por cálculo variacional y un principio de mínima acción permite obtener las ecuaciones del movimiento del sistema mediante derivación del Lagrangiano respecto a las coordenadas y a las velocidades, tal como se explica en cualquier manual avanzado sobre mecánica analítica.
Se trata fundamentalmente, por lo tanto, de postular correctamente dicha función de manera que el resultado de la simulación coincida con lo observado en el experimento.
En nuestra simulación, para obtener la órbita de la tierra alrededor del sol, el llamado problema de Kepler, hemos utilizado el Lagrangiano siguiente: donde r y φ son las coordenadas polares de la tierra respecto del sol. A éste le hemos sumado el Lagrangiano correspondiente al movimiento de rotación de la tierra, expresada anteriormente en (3), para obtener las trayectorias movimientos de nutación y precesión. Pero es, al añadir en L un término que correspondería a una fuerza central efectiva proporcional a Ω x v y que representaría la energía del movimiento postulado en la TID consistente en la variación de la dirección de la velocidad de traslación del cuerpo, pero no de su módulo, lo que permite a la simulación obtener el resultado más aproximado al observado, en lo que al movimiento de Chandler se refiere.
donde r y φ son las coordenadas polares de la tierra respecto del sol. A éste le hemos sumado el Lagrangiano correspondiente al movimiento de rotación de la tierra, expresada anteriormente en (3), para obtener las trayectorias movimientos de nutación y precesión. Pero es, al añadir en L un término que correspondería a una fuerza central efectiva proporcional a Ω x v y que representaría la energía del movimiento postulado en la TID consistente en la variación de la dirección de la velocidad de traslación del cuerpo, pero no de su módulo, lo que permite a la simulación obtener el resultado más aproximado al observado, en lo que al movimiento de Chandler se refiere.
Es necesario subrayar que esta fuerza central introducida en el Lagrangiano es, obviamente, ficticia y solo puede explicarse a través del acoplamiento de velocidades que se produce entre la velocidad de traslación del cuerpo (la v que aparece en el término añadido) y la velocidad de la partícula debida a la reacción dinámica del cuerpo y que da lugar al movimiento de precesión.
Por lo tanto, este término es en realidad el resultado del producto escalar: - (Ω x r). v = (Ω x v). r. Como vemos, al derivar esta expresión respecto de r se obtiene dicha fuerza central ficticia. El efecto de introducirlo es da lugar a la modificación de la trayectoria del objeto, en este caso la tierra, cambiando la dirección de la velocidad de traslación, pero no su módulo, de forma equivalente a lo expresado en la TID mediante la expresión: v = ᴪ.v0.
Como sabemos, el término mencionado que hemos añadido no está incorporado en la dinámica celeste aceptada académicamente. Nuestro objetivo es demostrar que su existencia, introduciéndolo en el Lagrangiano, mejora los datos obtenidos en la simulación respecto a la observación registrada.
Posteriormente, hemos incorporado a la función lagrangiana el resto de términos necesarios, como es el correspondiente al tirón gravitatorio de la luna. Finalmente, hemos afinado nuestro modelo teniendo en cuenta la forma de la tierra para obtener un valor más aproximado en la expresión del potencial gravitatorio de acuerdo a los libros de texto sobre el tema (ver “Fundamentos de Geofísica”, Agustín Udías y Julio Mezcua).
Como muestra de los resultados obtenidos en nuestra simulación, presentamos en el siguiente gráfico la curva obtenida por observación del movimiento de Chandler (Chandler´s Wobble en la denominación en inglés) a lo largo de 15 años (1992-2007):
Gráfica 1 A continuación, presentamos la curva obtenida mediante nuestra simulación y que podemos comparar con la anterior: 
En ambas gráficas aparece en el eje de ordenadas la coordenada angular, en radianes, correspondiente a la nutación y en el eje de abscisas el tiempo en segundos. La gráfica de la simulación (gráfica 2) representa el resultado obtenido a partir del modelo descrito aquí, es decir, corresponde al movimiento de nutación de Chandler de la tierra para cierto valor del parámetro R (distancia entre el centro de gravedad de la tierra y el eje de precesión, según la perpendicular al eje), cuyo valor desconocemos y que tendremos que evaluar al comparar con los datos reales.
Hemos presentado aquí esta gráfica porque de todas las simulaciones que hemos realizado variando dicho parámetro, su forma es la más parecida a la obtenida mediante observación (gráfica 1). Este parámetro aparece a partir del término antes mencionado: (Ω x r). v, al derivarlo respecto a la coordenada angular correspondiente a la precesión (ϕ), siendo Ω = dϕ /dt. Al integrar sobre el volumen, el valor de |r| se reduce a la distancia R entre el centro de gravedad, en el cual se aplica la velocidad de traslación de la tierra, y el eje de precesión de la misma, según la perpendicular.
Podemos observar en la gráfica de la simulación, que la amplitud máxima es 0,4089820 - 0,4089815 = 0,0000005 radianes = 0,103” (segundos de arco) que encaja muy bien con el valor esperado de 0,1“. En cuanto al periodo, vemos que hay 8 picos en un tiempo de 2x108 segundos = 6,34 años = 6 años y 4 meses, mientras que el valor registrado en la observación que aparece en la primera gráfica nos permite ver que entre 1993 y 2002, es decir, en 8 años y 6 meses, hay también 8 picos y por lo tanto existe una cierta desviación respecto al periodo esperado.
En cuanto al desplazamiento en el eje de ordenadas de la gráfica 2 con un valor de 0,4089 radianes respecto de la gráfica 1, se puede explicar al ser este valor justamente el ángulo de inclinación del eje de rotación respecto a la perpendicular al plano de la eclíptica, ya que este valor, al convertirlo a grados nos da aproximadamente los 23,27º (0,4061 radianes) correspondientes a dicha inclinación más los 9” (0,0025 radianes) correspondiente a la nutación producida por el tirón gravitatorio de la luna, tal como se describe en los textos, por ejemplo, en “Fundamentos de Geofísica” podemos leer:
“Además del movimiento de precesión, la inclinación de la órbita de la Luna respecto a la eclíptica (5ᵒ) produce un movimiento de nutación con un periodo principal de 18,6 años y amplitud de 9 segundos de arco”.
Por lo tanto, nuestro modelo describe muy bien el movimiento de nutación propio de la tierra, inducido por gravitación de los cuerpos celestes cercanos como son el sol y la luna, al poderse visualizar el desplazamiento en latitud de 9” mencionado anteriormente. En cuanto al segundo movimiento descrito en la literatura sobre el tema y conocido como movimiento de Chandler, aparece en nuestra simulación de forma natural, sin tener que postular un segundo movimiento de precesión y nutación en ausencia de pares externos (precesión libre).
Como hemos comentado, para obtener el valor más aproximado al observado es necesario incluir en el modelo el término correspondiente a una fuerza central ficticia, (Ω x r). v, en consonancia con la TID, y cuya presencia ni siquiera se considera en la teoría actual, tal como se acepta académicamente debido a que todos los fenómenos derivados se atribuyen al efecto Magnus. Veamos a continuación, como afecta a la simulación la eliminación del término mencionado.
Presentamos, en la siguiente gráfica, el resultado de la simulación para otro valor diferente del parámetro R, en la que está presente en el Lagrangiano el término correspondiente a la fuerza central ficticia descrita en la TID, para compararlo posteriormente con la simulación resultante de eliminar dicho término:
Observamos, en este caso, que el valor del periodo de nutación de Chandler está más en consonancia con el valor esperado de 10 picos (ciclos) en 9 años y seis meses = 3x108 segundos, respecto al caso anterior que hemos presentado en la gráfica 2.
Veamos ahora lo que obtenemos al eliminar de la simulación el término correspondiente a (Ω x r). v, siendo Ω la velocidad angular de precesión y v la velocidad de traslación de la tierra y r la distancia entre el eje de precesión y el centro de gravedad de la tierra, en el cual se aplica la velocidad de traslación. La siguiente gráfica corresponde a dicha simulación:
Vemos pues que, al eliminar el término mencionado, se ha perdido mucha precisión en lo que respecta al periodo de nutación de Chandler: solo observamos 6 picos frente a los 9 de la gráfica 3.
También la forma de la curva ha cambiado, siendo mucho menos parecida a lo observado en la realidad, tal como se muestra en la gráfica 1.
Conclusiones
En nuestra opinión, el presente estudio corrobora la validez de la Teoría de Interacciones Dinámicas al obtener, gracias a las ideas contenidas en ella, valores de la variación de la latitud producida por el movimiento de Chandler resultado de nuestra simulación, mucho más precisos que los obtenidos si no la tuviéramos en cuenta, constituyendo este hecho una evidencia importante a su favor.
(En cursiva el texto original de Arturo Rodriguez)
donde q1 = ϕ, q2 = θ, q3 = ψ son los ángulos de Euler.
En nuestro estudio, vamos a analizar particularmente el caso f descrito en el documento A:
Figura 3
En esta gráfica podemos observar el amortiguamiento del valor de la velocidad angular de nutación (dθ/dt) hasta un valor constante indicado en la figura por Δθ. El autor del experimento achaca este fenómeno a la acción rozamiento del giróscopo con la pieza de apoyo o cojinete que lo sujeta, que se podría simular en el programa introduciendo en las ecuaciones de la dinámica un término proporcional a la derivada de la componente de la velocidad angular correspondiente a la nutación.
Sin embargo, la fricción es un proceso físico no conservativo y, por tanto, debería afectar al movimiento de rotación en su conjunto y no solamente a una de sus componentes, ya que en ese caso se manifestaría un comportamiento selectivo que no se puede justificar. Sin embargo, en nuestro modelo, esta amortiguación se produce de forma natural, sin contradecir principios como la segunda ley de la termodinámica; recordemos que las fuerzas conservativas aumentan la entropía del sistema, lo cual se contradice con la supresión selectiva del movimiento de nutación, debido a que ésta supondría un mayor orden estructural en lo que a la dinámica del cuerpo se refiere.
Para llegar a esto fue necesario realizar modificaciones en el modelo teórico convencional, tal como fue simulado originalmente y que da lugar a la curva en azul de la gráfica de la figura 3. La curva en rojo corresponde al valor obtenido experimentalmente en el laboratorio. Pues bien, en nuestra gráfica de la figura 4 presentamos en color rojo la curva correspondiente al valor predicho por nuestra teoría y mantenemos el color azul para visualizar la curva obtenida por el método convencionalmente aceptado, que ya hemos descrito anteriormente.
Figura 4
Podemos observar en esta gráfica, resultado de nuestra simulación, un valor predicho teóricamente muy próximo al valor real observado, si la comparamos con la curva en rojo de la figura 3. Lo interesante es que, el hecho de que la nutación esté prácticamente suprimida de forma natural sin tener que apelar a las fuerzas de rozamiento, concuerda con la observación del movimiento de la tierra. Esto encajaría con nuestro modelo, al no existir apoyo alguno que amortigüe este fenómeno y siendo el movimiento de nutación medido de un orden muy pequeño, hasta el punto de que apenas tiene influencia sobre la tierra. Es un hecho probado la poca incidencia que tiene el movimiento de nutación en este tipo de fenómenos, en los cuales pasa casi desapercibido. En nuestro modelo este amortiguamiento se puede justificar sin necesidad de añadir hipótesis, como es la posibilidad de que esto sea debido al rozamiento que afectaría a la nutación de forma selectiva, como hemos comentado anteriormente. Sería interesante realizar experimentos en vacío que corroboren lo que postulamos aquí.
Antes de desarrollar las ecuaciones de nuestra teoría, es conveniente recordar los conceptos de la física actual con los que, de forma comúnmente aceptada, se analiza el problema en cuestión. Por una parte, tenemos las ecuaciones de Euler para la dinámica rotacional del sólido rígido que, aparentemente se derivan de la conservación del momento angular total del cuerpo, sumando de forma arbitraria la acción de pares de fuerza no coaxiales. En nuestra teoría, el momento angular está disociado en dos vectores independientes, cada uno de ellos está asociado a uno solo de los torques no coaxiales y que forman parte se sistemas de ecuaciones independientes, aunque acoplados a través de otras variables comunes que aparecen en ambos sistemas.
Esto se logra mediante la separación de la parte real y de la parte compleja en las igualdades que aparecen en las ecuaciones del movimiento. Este procedimiento no es el habitual en mecánica clásica, donde solo se consideran valores reales, mientras que los imaginarios se rechazan por “no físicos”.
En la actualidad, la versión relativista de la mecánica postula que las todas las aceleraciones, incluidas las inerciales, son equivalentes a un campo gravitatorio, en lo que se conoce como principio de equivalencia fuerte y que fue postulado por Einstein en su teoría de la relatividad general.
Nosotros coincidimos con los principios d la TID que sostienen que dichas aceleraciones deberían estar fuera del principio de equivalencia, el cual tendría que estar solamente referido a aceleraciones lineales que no generen rotación, dejando así un principio de equivalencia débil más limitado y que permita situar el problema que estamos tratando dentro de un marco más extenso. Desde nuestro punto de vista, dicha extensión se basaría en la posibilidad de incluir funciones y números complejos para modelar la realidad física.
Coincidimos plenamente con lo expresado en el artículo del autor de la TID: ”ON THE EQUIVALENCE PRINCIPLE” en el sentido de que un observador sí que podría distinguir, respecto de un campo gravitatorio, los efectos producidos por pares de fuerzas no coaxiales en un cuerpo por las razones que en dicho artículo se describen.
Como consecuencia, el sacar estos fenómenos fuera del marco del principio de equivalencia, implicaría postular una nueva simetría distinta a la empleada en la relatividad general, que es conocida como el grupo de difeomorfismos y que viene a decir que las ecuaciones de campo de la gravedad son invariantes ante cualquier cambio del sistema de coordenadas definido por el tensor métrico.
Si queremos postular una nueva teoría alternativa a la actualmente aceptada, tendremos que demostrar que dicha teoría está gobernada por cierto grupo de simetría distinto, aún por descubrir y que, por analogía con otros fenómenos físicos sería lógico que fuera una simetría de tipo gauge. En nuestro caso, habría que buscar la invariancia del sistema físico al ser sometido a diversas modificaciones en los valores de las cargas de pares de fuerzas, en lugar de fuerza tal como se suele interpretar. (ver la entrada sobre “simetría de gauge” en Wikipedia). Veremos más adelante que el grupo de simetría de gauge de nuestra teoría es el SO(4)/Z2.
Antes de entrar en detalles sobre el desarrollo matemático de nuestra teoría, procedemos a continuación a resumir brevemente el movimiento de Chandler que experimenta la tierra como consecuencia de su movimiento de rotación-precesión-nutación.
Por un lado, la tierra gira sobre un eje en un movimiento que denominamos rotación intrínseca, causa de que haya días y noches. Desde la antigüedad se sabe también que nuestro planeta experimenta un movimiento llamado “precesión de los equinoccios” y que consiste, básicamente, en el giro del eje de rotación alrededor otro eje, describiendo, por tanto, la trayectoria del eje de rotación intrínseca la superficie de un cono.
Dicha trayectoria puede sufrir a su vez oscilaciones periódicas alrededor de un tercer eje perpendicular a los anteriores, dando lugar al movimiento conocido como nutación. El par que produce estos movimientos consiste en la atracción gravitatoria simultánea del sol y la luna sobre el abultamiento del planeta en el ecuador. También influye la atracción de los planetas.
El conocimiento de la precesión de los equinoccios ha sido muy importante históricamente, especialmente en navegación, ya que dicho movimiento modifica el lugar (se considera, en realidad, la estrella más cercana a ese lugar) al que apunta el eje de rotación. Actualmente, apunta a la estrella polar, pero en tiempos remotos el punto exacto estaba considerablemente desviado de ésta y en el futuro apuntará a otra estrella distinta: Vega. Como sabemos, este movimiento es extraordinariamente lento comparado con el de rotación.
Simultáneamente, todavía existe un segundo movimiento de precesión y nutación experimentado por la tierra, probablemente ya conocido desde la antigüedad, ya que da lugar a variaciones del orden de décimas de segundos de arco, lo cual produce un error no despreciable en cálculos para navegación y que, en principio no se podía justificar mediante torques producidos por la gravedad de newton. Este fenómeno fue aparentemente explicado en principio por Euler en siglo XVIII al considerar que era el resultado de sus famosas ecuaciones del movimiento rotacional del sólido rígido en ausencia de pares fe fuerzas.
A este fenómeno lo denominó precesión y nutación libres, con un periodo de unos diez meses de la variación de la latitud, según sus cálculos. La verificación experimental y análisis de este movimiento se lleva a cabo en el siglo XIX por S.C. Chandler y desde entonces lleva su nombre. El valor del periodo obtenido en sus medidas dio como resultado 428 días, un 40 por ciento mayor del esperado respecto al dado por Euler.
Actualmente, se ha medido con gran precisión un periodo de 436 días y una amplitud aproximadamente de 0,1 segundos de arco. Finalmente, el astrónomo Newcomb achaca esta diferencia a la no rigidez de la tierra y postula la existencia de dos periodos independientes: uno propio de Chandler y otro anual producido por variaciones de masas de la atmósfera.
Sin embargo, lo que nos llama la atención es que, para explicar este fenómeno, se utilice un segundo sistema de ecuaciones de Euler para torques nulos, independiente del necesario para explicar la precesión de los equinoccios para torques producidos por fuerzas gravitacionales procedentes del sol y la luna, ya que se están utilizando dos variables distintas, correspondientes a dos momentos angulares diferentes, aplicados en el mismo objeto. Pero esto va en contra de la propia teoría clásica aceptada, ya que dichos momentos se sumarían vectorialmente.
Actualmente, en mecánica clásica se acepta, en nuestra opinión errónea y arbitrariamente, que los momentos angulares correspondientes a torques aplicados en el cuerpo según ejes no coaxiales se pueden sumar algebraicamente, tal como se hace con otras magnitudes vectoriales, como las fuerzas aplicadas a un cuerpo en el centro de gravedad.
Por eso nos sorprende tanto que, en el problema que estamos tratando sobre el movimiento rotacional de la tierra, no se aplique ese mismo criterio y se postulen dos vectores distintos, por una parte, para el momento angular que produce la precesión inducida por el tirón gravitatorio de objetos celestes cercanos y, por otra, un momento angular diferente asociado a la llamada precesión libre, que daría lugar al movimiento de Chandler y con una de las componentes común a ambos casos correspondiente a la rotación intrínseca.
Quizás para disimular, de alguna manera, esta falta de coherencia teórica, se denomina en la literatura sobre el tema “precesión de los equinoccios” al primer fenómeno y “nutación de Chandler” al segundo, cuando en realidad ambos movimientos presentan al mismo tiempo tanto precesión como nutación de forma simultánea.
Sin embargo, es interesante remarcar que en nuestro modelo sí que es posible tener vectores de momento angular independientes siempre que aparezcan en forma compleja; uno como la parte real y el otro la parte imaginaria. Posteriormente, al elevar al cuadrado las magnitudes correspondientes para obtener la función Lagrangiana del sistema, el numero imaginario desaparece ya que su valor al cuadrado es -1. Así tenemos que, manejando magnitudes complejas, al final solo aparecen números reales en las ecuaciones del movimiento.
ste procedimiento es que llevamos a cabo para proceder a la simulación de nuestra teoría mediante un programa informático en el entorno de programación en lenguaje Maple, que se puede utilizar para resolver en el ordenador sistemas de ecuaciones diferenciales, entre otras muchas utilidades matemáticas.
El modelo físico del sistema que estamos estudiando se puede implementar mediante la llamada aproximación lagrangiana, consistente en partir de una función de las coordenadas y las velocidades que por cálculo variacional y un principio de mínima acción permite obtener las ecuaciones del movimiento del sistema mediante derivación del Lagrangiano respecto a las coordenadas y a las velocidades, tal como se explica en cualquier manual avanzado sobre mecánica analítica.
Se trata fundamentalmente, por lo tanto, de postular correctamente dicha función de manera que el resultado de la simulación coincida con lo observado en el experimento.
En nuestra simulación, para obtener la órbita de la tierra alrededor del sol, el llamado problema de Kepler, hemos utilizado el Lagrangiano siguiente:
Es necesario subrayar que esta fuerza central introducida en el Lagrangiano es, obviamente, ficticia y solo puede explicarse a través del acoplamiento de velocidades que se produce entre la velocidad de traslación del cuerpo (la v que aparece en el término añadido) y la velocidad de la partícula debida a la reacción dinámica del cuerpo y que da lugar al movimiento de precesión.
Por lo tanto, este término es en realidad el resultado del producto escalar: - (Ω x r). v = (Ω x v). r. Como vemos, al derivar esta expresión respecto de r se obtiene dicha fuerza central ficticia. El efecto de introducirlo es da lugar a la modificación de la trayectoria del objeto, en este caso la tierra, cambiando la dirección de la velocidad de traslación, pero no su módulo, de forma equivalente a lo expresado en la TID mediante la expresión: v = ᴪ.v0.
Como sabemos, el término mencionado que hemos añadido no está incorporado en la dinámica celeste aceptada académicamente. Nuestro objetivo es demostrar que su existencia, introduciéndolo en el Lagrangiano, mejora los datos obtenidos en la simulación respecto a la observación registrada.
Posteriormente, hemos incorporado a la función lagrangiana el resto de términos necesarios, como es el correspondiente al tirón gravitatorio de la luna. Finalmente, hemos afinado nuestro modelo teniendo en cuenta la forma de la tierra para obtener un valor más aproximado en la expresión del potencial gravitatorio de acuerdo a los libros de texto sobre el tema (ver “Fundamentos de Geofísica”, Agustín Udías y Julio Mezcua).
Como muestra de los resultados obtenidos en nuestra simulación, presentamos en el siguiente gráfico la curva obtenida por observación del movimiento de Chandler (Chandler´s Wobble en la denominación en inglés) a lo largo de 15 años (1992-2007):
Gráfica 1
Gráfica 2
Se puede observar que la gráfica 2 está desplazada unos 0,4 radianes respecto al eje vertical por razones que se explicarán posteriormente. Lo importante ahora es ver las coincidencias, tanto en amplitud como en período, así como en la forma de las curvas. En ambas gráficas aparece en el eje de ordenadas la coordenada angular, en radianes, correspondiente a la nutación y en el eje de abscisas el tiempo en segundos. La gráfica de la simulación (gráfica 2) representa el resultado obtenido a partir del modelo descrito aquí, es decir, corresponde al movimiento de nutación de Chandler de la tierra para cierto valor del parámetro R (distancia entre el centro de gravedad de la tierra y el eje de precesión, según la perpendicular al eje), cuyo valor desconocemos y que tendremos que evaluar al comparar con los datos reales.
Hemos presentado aquí esta gráfica porque de todas las simulaciones que hemos realizado variando dicho parámetro, su forma es la más parecida a la obtenida mediante observación (gráfica 1). Este parámetro aparece a partir del término antes mencionado: (Ω x r). v, al derivarlo respecto a la coordenada angular correspondiente a la precesión (ϕ), siendo Ω = dϕ /dt. Al integrar sobre el volumen, el valor de |r| se reduce a la distancia R entre el centro de gravedad, en el cual se aplica la velocidad de traslación de la tierra, y el eje de precesión de la misma, según la perpendicular.
Podemos observar en la gráfica de la simulación, que la amplitud máxima es 0,4089820 - 0,4089815 = 0,0000005 radianes = 0,103” (segundos de arco) que encaja muy bien con el valor esperado de 0,1“. En cuanto al periodo, vemos que hay 8 picos en un tiempo de 2x108 segundos = 6,34 años = 6 años y 4 meses, mientras que el valor registrado en la observación que aparece en la primera gráfica nos permite ver que entre 1993 y 2002, es decir, en 8 años y 6 meses, hay también 8 picos y por lo tanto existe una cierta desviación respecto al periodo esperado.
En cuanto al desplazamiento en el eje de ordenadas de la gráfica 2 con un valor de 0,4089 radianes respecto de la gráfica 1, se puede explicar al ser este valor justamente el ángulo de inclinación del eje de rotación respecto a la perpendicular al plano de la eclíptica, ya que este valor, al convertirlo a grados nos da aproximadamente los 23,27º (0,4061 radianes) correspondientes a dicha inclinación más los 9” (0,0025 radianes) correspondiente a la nutación producida por el tirón gravitatorio de la luna, tal como se describe en los textos, por ejemplo, en “Fundamentos de Geofísica” podemos leer:
“Además del movimiento de precesión, la inclinación de la órbita de la Luna respecto a la eclíptica (5ᵒ) produce un movimiento de nutación con un periodo principal de 18,6 años y amplitud de 9 segundos de arco”.
Por lo tanto, nuestro modelo describe muy bien el movimiento de nutación propio de la tierra, inducido por gravitación de los cuerpos celestes cercanos como son el sol y la luna, al poderse visualizar el desplazamiento en latitud de 9” mencionado anteriormente. En cuanto al segundo movimiento descrito en la literatura sobre el tema y conocido como movimiento de Chandler, aparece en nuestra simulación de forma natural, sin tener que postular un segundo movimiento de precesión y nutación en ausencia de pares externos (precesión libre).
Como hemos comentado, para obtener el valor más aproximado al observado es necesario incluir en el modelo el término correspondiente a una fuerza central ficticia, (Ω x r). v, en consonancia con la TID, y cuya presencia ni siquiera se considera en la teoría actual, tal como se acepta académicamente debido a que todos los fenómenos derivados se atribuyen al efecto Magnus. Veamos a continuación, como afecta a la simulación la eliminación del término mencionado.
Presentamos, en la siguiente gráfica, el resultado de la simulación para otro valor diferente del parámetro R, en la que está presente en el Lagrangiano el término correspondiente a la fuerza central ficticia descrita en la TID, para compararlo posteriormente con la simulación resultante de eliminar dicho término:
Gráfica 3
Observamos, en este caso, que el valor del periodo de nutación de Chandler está más en consonancia con el valor esperado de 10 picos (ciclos) en 9 años y seis meses = 3x108 segundos, respecto al caso anterior que hemos presentado en la gráfica 2.
Veamos ahora lo que obtenemos al eliminar de la simulación el término correspondiente a (Ω x r). v, siendo Ω la velocidad angular de precesión y v la velocidad de traslación de la tierra y r la distancia entre el eje de precesión y el centro de gravedad de la tierra, en el cual se aplica la velocidad de traslación. La siguiente gráfica corresponde a dicha simulación:
Gráfica 4
Vemos pues que, al eliminar el término mencionado, se ha perdido mucha precisión en lo que respecta al periodo de nutación de Chandler: solo observamos 6 picos frente a los 9 de la gráfica 3.
También la forma de la curva ha cambiado, siendo mucho menos parecida a lo observado en la realidad, tal como se muestra en la gráfica 1.
Conclusiones
En nuestra opinión, el presente estudio corrobora la validez de la Teoría de Interacciones Dinámicas al obtener, gracias a las ideas contenidas en ella, valores de la variación de la latitud producida por el movimiento de Chandler resultado de nuestra simulación, mucho más precisos que los obtenidos si no la tuviéramos en cuenta, constituyendo este hecho una evidencia importante a su favor.
(En cursiva el texto original de Arturo Rodriguez)
Gabriel Barceló
27/05/2020
Comentarios
Noticias de Física
Gabriel Barcelo y Arturo Rodriguez
Ya nos hemos referido a un amigo y antiguo colaborador, Arturo Rodriguez, y a sus estudios, en los que sugiere claves para confirmar la TID. Uno de los últimos trabajos realizados es un análisis del llamado bamboleo de Chandler, que le ocurre a nuestro planeta Tierra. Según fue observado por Seth Carlo Chandler en 1891, se genera constantemente una pequeña variación en la posición del eje de rotación de la Tierra. Arturo ha propuesto que este movimiento puede explicarse más fácilmente a partir de la Teoría de Interacciones Dinámicas. Veamos su estudio.
El bamboleo se ha estimado en una variación de 0,7 segundos de arco en un período de 433 días, de tal forma que los polos de la Tierra oscilan, generando una circunferencia irregular de 3 a 15 metros de diámetro. Este movimiento se añade al de precesión de los equinoccios, y a los de nutación, rotación y traslación de la Tierra. Tradicionalmente no se ha podido justificar su origen, no obstante, en 2000 el Jet Propulsion Laboratory (Laboratorio de Propulsión a Chorro) de la NASA anunció que la supuesta causa principal del bamboleo de Chandler es la presión fluctuante del fondo oceánico, originada por los cambios en la temperatura y la salinidad, y por los cambios en la dirección de las corrientes oceánicas. No obstante, esta hipótesis todavía está en estudio por la comunidad científica
Ya publicamos trabajos de Arturo Rodriguez en estas páginas el pasado año:
https://www.tendencias21.net/fisica/Nuevos-avances-en-dinamica-rotacional-I_a79.html
https://www.tendencias21.net/fisica/Nuevos-avances-en-dinamica-rotacional-II_a80.html
Vamos a conocer la propuesta del ingeniero Arturo Rodriguez.
Introducción a la Teoría de Campos Giroscópicos
En el presente documento, vamos a describir una serie de ideas alternativas a la actualmente aceptada teoría del movimiento rotatorio basada en las ecuaciones de Euler. Dichas ideas van a permitir interpretar fenómenos observables, como es el llamado movimiento de Chandler que experimenta la tierra, como veremos mediante simulaciones por ordenador de las ecuaciones postuladas. Al mismo tiempo intentaremos demostrar que estas ideas coinciden con las expresadas en la “Teoría de Interacciones Dinámicas” (TID), a las que habríamos llegado por otros caminos, ya que nos hemos basado, al realizar el diseño del modelo matemático propuesto aquí, en el hecho de que debe existir una clara correspondencia entre la TID y nuestra propuesta, a la que llamaremos en adelante: “Teoría de Campos Giroscópicos” (TCG).
Hemos elegido este nombre porque se encuadra en el mismo marco que las ecuaciones de Navier-Stokes de la Dinámica de Fluidos. Es decir, nosotros no partimos de la cinemática del punto material de masa m, sino del concepto de partícula fluida de densidad ᵨ. A partir de aquí, hemos construido una teoría de campos basada en la aplicación de los operadores diferenciales característicos de estas teorías (el rotacional, la divergencia, etc…). Consideramos que la estructura matemática de la teoría no debe depender del estado de agregación de la materia que presente el objeto y que este se manifiesta solamente a través del valor de sus parámetros (viscosidad, etc…). Finalmente, integrando espacialmente las ecuaciones y teniendo en cuenta las condiciones de contorno que impone el objeto físico, se llegará a la solución del problema.
Teoría de Interacciones Dinámicas y Teoría de Campos Giroscópicos
La primera idea que vamos a introducir es la de “Inercia Rotacional”, ya postulada en la TID, donde ya está suficientemente descrita en la bibliografía. Es un concepto muy intuitivo si se está ya familiarizado con el equivalente para el movimiento lineal: la inercia de la materia, tal como la conocemos. Desde nuestro punto de vista, la incorporación de este concepto a la dinámica da lugar a la necesidad de separar el movimiento de rotación intrínseco, respecto a los otros movimientos reflejados en la cinemática descrita por los ángulos de Euler: la precesión y la nutación, ya que dicha inercia solo afectaría al primero. En nuestra teoría, no concebimos tal descomposición de movimientos, donde se parte de un único vector de velocidad angular y cuyas tres componentes corresponden a rotación, precesión y nutación, respectivamente.
Postulamos, por tanto, la existencia de dos vectores independientes: W y Ω, que serían perpendiculares entre sí. El primero corresponde a la rotación intrínseca y el segundo a la composición de los movimientos de precesión y de nutación. Estos dos vectores no se pueden sumar algebraicamente, de lo contrario volveríamos al modelo de ángulos de Euler. La única posibilidad que nos queda, es definir una estructura matemática en forma de función compleja: W + i Ω donde el primer término es Ω la parte real de la función y el segundo término representa la parte imaginaria, e i es raíz cuadrada de -1.
Esto podría parecer, en principio, un simple truco matemático sin ningún fundamento que lo sostenga. Veremos, a continuación, como el concepto de Holonomía (junto al concepto de simetría basada en Grupos de Lie) perteneciente a la geometría diferencial, va a suministrarnos los principios fundamentales para sostener nuestro modelo matemático.
El concepto de Holonomía se puede definir como una característica de la geometría diferencial que “mide como el transporte paralelo alrededor de lazos cerrados no preserva los datos geométricos que se transportan”. En nuestro caso, esta idea se identificaría con el ángulo formado por el vector tangente (es decir, la velocidad de la partícula) que forma consigo mismo después de haber sido transportado paralelamente 360 grados, correspondientes a un lazo cerrado (2π radianes). La Holonomía de la conexión puede ser identificada con un grupo de Lie, que podríamos denominar el “Grupo de Holonomía” de la teoría.
El grupo de Holonomía (o simplemente Grupo de Simetría) comúnmente aceptado en la cinemática de sólido rígido, descrita mediante ángulos de Euler, es el grupo de Lie SO (3), es decir, el grupo convencional de las rotaciones en tres dimensiones.
Ya publicamos trabajos de Arturo Rodriguez en estas páginas el pasado año:
https://www.tendencias21.net/fisica/Nuevos-avances-en-dinamica-rotacional-I_a79.html
https://www.tendencias21.net/fisica/Nuevos-avances-en-dinamica-rotacional-II_a80.html
Vamos a conocer la propuesta del ingeniero Arturo Rodriguez.
Introducción a la Teoría de Campos Giroscópicos
En el presente documento, vamos a describir una serie de ideas alternativas a la actualmente aceptada teoría del movimiento rotatorio basada en las ecuaciones de Euler. Dichas ideas van a permitir interpretar fenómenos observables, como es el llamado movimiento de Chandler que experimenta la tierra, como veremos mediante simulaciones por ordenador de las ecuaciones postuladas. Al mismo tiempo intentaremos demostrar que estas ideas coinciden con las expresadas en la “Teoría de Interacciones Dinámicas” (TID), a las que habríamos llegado por otros caminos, ya que nos hemos basado, al realizar el diseño del modelo matemático propuesto aquí, en el hecho de que debe existir una clara correspondencia entre la TID y nuestra propuesta, a la que llamaremos en adelante: “Teoría de Campos Giroscópicos” (TCG).
Hemos elegido este nombre porque se encuadra en el mismo marco que las ecuaciones de Navier-Stokes de la Dinámica de Fluidos. Es decir, nosotros no partimos de la cinemática del punto material de masa m, sino del concepto de partícula fluida de densidad ᵨ. A partir de aquí, hemos construido una teoría de campos basada en la aplicación de los operadores diferenciales característicos de estas teorías (el rotacional, la divergencia, etc…). Consideramos que la estructura matemática de la teoría no debe depender del estado de agregación de la materia que presente el objeto y que este se manifiesta solamente a través del valor de sus parámetros (viscosidad, etc…). Finalmente, integrando espacialmente las ecuaciones y teniendo en cuenta las condiciones de contorno que impone el objeto físico, se llegará a la solución del problema.
Teoría de Interacciones Dinámicas y Teoría de Campos Giroscópicos
La primera idea que vamos a introducir es la de “Inercia Rotacional”, ya postulada en la TID, donde ya está suficientemente descrita en la bibliografía. Es un concepto muy intuitivo si se está ya familiarizado con el equivalente para el movimiento lineal: la inercia de la materia, tal como la conocemos. Desde nuestro punto de vista, la incorporación de este concepto a la dinámica da lugar a la necesidad de separar el movimiento de rotación intrínseco, respecto a los otros movimientos reflejados en la cinemática descrita por los ángulos de Euler: la precesión y la nutación, ya que dicha inercia solo afectaría al primero. En nuestra teoría, no concebimos tal descomposición de movimientos, donde se parte de un único vector de velocidad angular y cuyas tres componentes corresponden a rotación, precesión y nutación, respectivamente.
Postulamos, por tanto, la existencia de dos vectores independientes: W y Ω, que serían perpendiculares entre sí. El primero corresponde a la rotación intrínseca y el segundo a la composición de los movimientos de precesión y de nutación. Estos dos vectores no se pueden sumar algebraicamente, de lo contrario volveríamos al modelo de ángulos de Euler. La única posibilidad que nos queda, es definir una estructura matemática en forma de función compleja: W + i Ω donde el primer término es Ω la parte real de la función y el segundo término representa la parte imaginaria, e i es raíz cuadrada de -1.
Esto podría parecer, en principio, un simple truco matemático sin ningún fundamento que lo sostenga. Veremos, a continuación, como el concepto de Holonomía (junto al concepto de simetría basada en Grupos de Lie) perteneciente a la geometría diferencial, va a suministrarnos los principios fundamentales para sostener nuestro modelo matemático.
El concepto de Holonomía se puede definir como una característica de la geometría diferencial que “mide como el transporte paralelo alrededor de lazos cerrados no preserva los datos geométricos que se transportan”. En nuestro caso, esta idea se identificaría con el ángulo formado por el vector tangente (es decir, la velocidad de la partícula) que forma consigo mismo después de haber sido transportado paralelamente 360 grados, correspondientes a un lazo cerrado (2π radianes). La Holonomía de la conexión puede ser identificada con un grupo de Lie, que podríamos denominar el “Grupo de Holonomía” de la teoría.
El grupo de Holonomía (o simplemente Grupo de Simetría) comúnmente aceptado en la cinemática de sólido rígido, descrita mediante ángulos de Euler, es el grupo de Lie SO (3), es decir, el grupo convencional de las rotaciones en tres dimensiones.
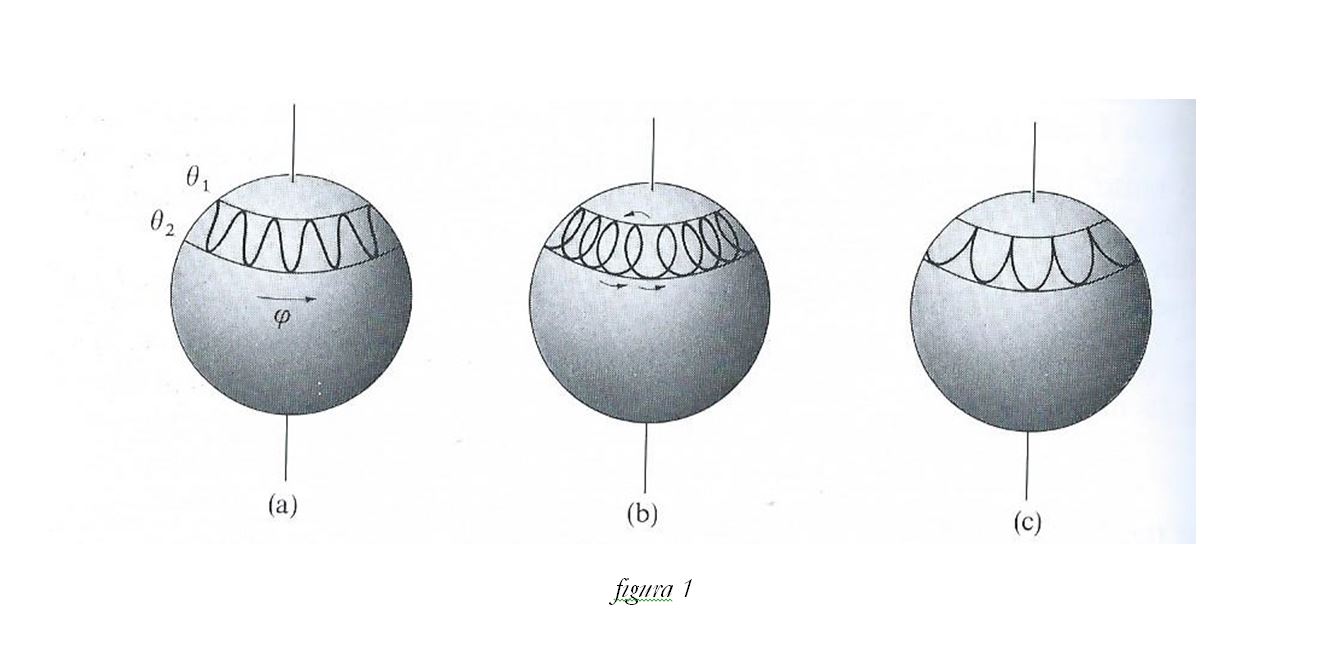
En nuestro modelo, este no es el grupo correcto, como se puede comprobar en la figura 2, que representa el movimiento de precesión y nutación de un giróscopo real, ya que la trayectoria del eje de rotación (para ser más exactos, su proyección a lo largo de una esfera, ver figura 1) no coincide con el observado en el experimento. Puede observase cierto desfase entre ambas curvas. Esto quiere decir que las herramientas geometro-diferenciales suministradas por SO (3), tal como se acepta en la actualidad, no son las adecuadas para describir el problema y será necesario, por tanto, postular un grupo de simetría más extenso y que lo contenga, al ser éste una buena aproximación al problema como lo demuestra el hecho de que su utilización en ciencia y tecnología está totalmente aceptado.
Nosotros lo que postulamos aquí es que el modelo de Euler, aun siendo útil en ingeniería (donde el movimiento de precesión está suprimido por el eje en la mayoría de los casos, como robots, etc…), no es el definitivo. Después de una serie de modificaciones en la estructura matemática del modelo descrito mediante el Lagrangiano del sistema, hemos llegado a la conclusión de que el verdadero grupo de Holonomía debería ser el SO (4) / Z2, donde Z2 representa el grupo de permutaciones de dos elementos y la barra representa el cociente entre los dos. Es interesante observar que a este grupo se le puede considerar como el que describe la simetría del problema de Kepler (ver página https://en.wikipedia.org/wiki/Laplace%E2%80%93Runge%E2%80%93Lenz_vector ). Veremos que esto va a permitir un marco conceptual adecuado a la hora de simular los movimientos simultáneos de rotación y órbitación alrededor del sol, producidos por la gravitación newtoniana, y que nos va a suministrar las herramientas necesarias para simular los movimientos de precesión y nutación de la tierra y, por tanto, el movimiento de Chandler.
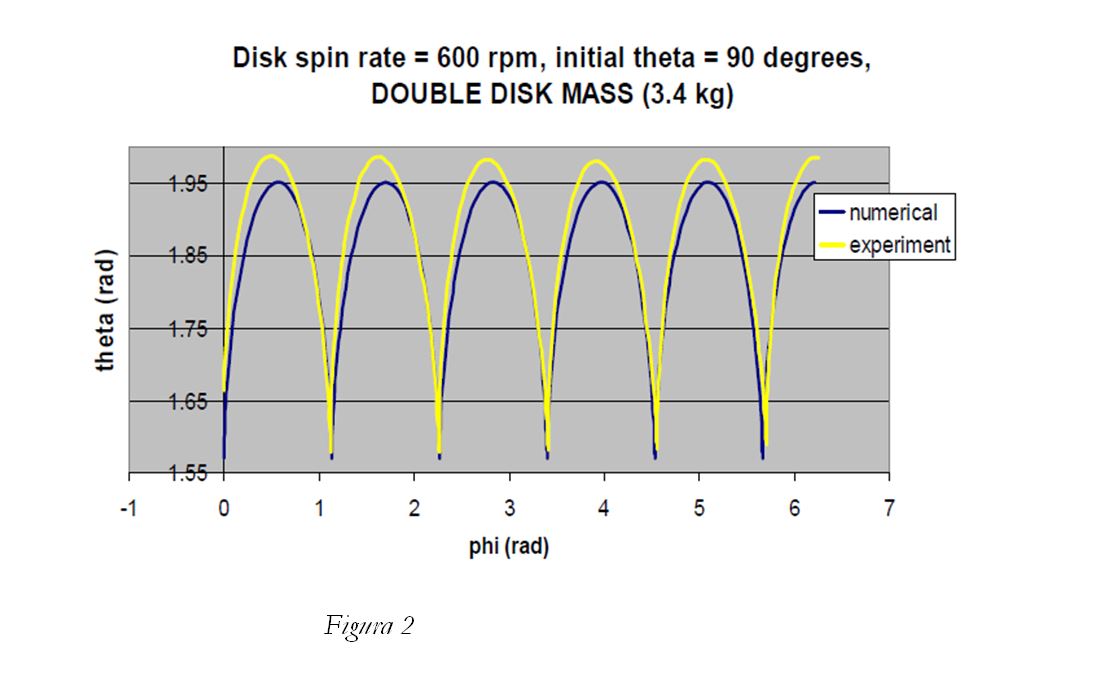
La siguiente figura, la cual hemos mencionado anteriormente, representa la variación del ángulo de nutación theta (θ) respecto del ángulo de precesión phi (ϕ), descritos ambos en la figura 1, obtenido en un experimento en el laboratorio. Como vemos el desfase obtenido entre el valor predicho por la teoría convencional (en azul) cuyo grupo de simetría es el SO (3) y el valor observado (en amarillo), aunque pequeño en apariencia, es reseñable ya que se deduce que, por acumulación del error, las curvas se desfasarán enormemente después de muchos ciclos. (En cursiva el texto original de Arturo Rodriguez)
Nosotros lo que postulamos aquí es que el modelo de Euler, aun siendo útil en ingeniería (donde el movimiento de precesión está suprimido por el eje en la mayoría de los casos, como robots, etc…), no es el definitivo. Después de una serie de modificaciones en la estructura matemática del modelo descrito mediante el Lagrangiano del sistema, hemos llegado a la conclusión de que el verdadero grupo de Holonomía debería ser el SO (4) / Z2, donde Z2 representa el grupo de permutaciones de dos elementos y la barra representa el cociente entre los dos. Es interesante observar que a este grupo se le puede considerar como el que describe la simetría del problema de Kepler (ver página https://en.wikipedia.org/wiki/Laplace%E2%80%93Runge%E2%80%93Lenz_vector ). Veremos que esto va a permitir un marco conceptual adecuado a la hora de simular los movimientos simultáneos de rotación y órbitación alrededor del sol, producidos por la gravitación newtoniana, y que nos va a suministrar las herramientas necesarias para simular los movimientos de precesión y nutación de la tierra y, por tanto, el movimiento de Chandler.
La siguiente figura, la cual hemos mencionado anteriormente, representa la variación del ángulo de nutación theta (θ) respecto del ángulo de precesión phi (ϕ), descritos ambos en la figura 1, obtenido en un experimento en el laboratorio. Como vemos el desfase obtenido entre el valor predicho por la teoría convencional (en azul) cuyo grupo de simetría es el SO (3) y el valor observado (en amarillo), aunque pequeño en apariencia, es reseñable ya que se deduce que, por acumulación del error, las curvas se desfasarán enormemente después de muchos ciclos. (En cursiva el texto original de Arturo Rodriguez)
Editado por
Gabriel Barceló

Gabriel Barceló es actualmente uno de los miembros directivos del Club Nuevo Mundo, impulsado por Tendencias21. Es Dr. Ingeniero industrial y estudio la licenciatura de Ciencias Físicas.
Fue durante veinte años funcionario del Ministerio de Hacienda, como Inspector de Finanzas del Estado, Subdirector del Centro de Proceso de Datos del Ministerio de Hacienda, Inspector Jefe de Madrid y fundador y presidente de la Asociación profesional de Inspectores de Hacienda, representativa del Cuerpo Superior de Inspectores de Hacienda del Estado (Actualmente: Inspectores de Hacienda del Estado: IHE).
Posteriormente causó baja como funcionario, y fue fundador y presidente de diversas empresas, de asociaciones no lucrativas y de fundaciones, actuando como presidente de las mismas, ex-Presidente de la Federación de Ingenieros Industriales de España y ex-Vicepresidente del Instituto de la Ingeniería de España, Gabriel Barceló ha sido consultor en ingeniería de la edificación y asesor fiscal.
Desde hace más de treinta y seis años desarrolla un proyecto de investigación científica sobre dinámica rotacional. Autor de numerosos libros, destacando: “Nuevo paradigma en Física” (editado en inglés y español, en dos tomos), y ha publicado más de cien artículos.
Fue durante veinte años funcionario del Ministerio de Hacienda, como Inspector de Finanzas del Estado, Subdirector del Centro de Proceso de Datos del Ministerio de Hacienda, Inspector Jefe de Madrid y fundador y presidente de la Asociación profesional de Inspectores de Hacienda, representativa del Cuerpo Superior de Inspectores de Hacienda del Estado (Actualmente: Inspectores de Hacienda del Estado: IHE).
Posteriormente causó baja como funcionario, y fue fundador y presidente de diversas empresas, de asociaciones no lucrativas y de fundaciones, actuando como presidente de las mismas, ex-Presidente de la Federación de Ingenieros Industriales de España y ex-Vicepresidente del Instituto de la Ingeniería de España, Gabriel Barceló ha sido consultor en ingeniería de la edificación y asesor fiscal.
Desde hace más de treinta y seis años desarrolla un proyecto de investigación científica sobre dinámica rotacional. Autor de numerosos libros, destacando: “Nuevo paradigma en Física” (editado en inglés y español, en dos tomos), y ha publicado más de cien artículos.
Archivo
Últimos posts
Enlaces de interés
Tendencias científicas
Tags
25th International Conference on High Resolution Molecular Spectroscopy
CSIC
asociaciones mundiales. organización de la ingenieria
Dinámica
Dinámica. Teoría de Interacciones dinámicas. Dinámica rotacional
Dinámica. Teoría de Interacciones dinámicas. Dinámica rotacional
Emprendimiento
Dinámica. Teoría de Interacciones dinámicas. Dinámica rotacional
Emprendimiento
Empresa
Empresa
ETSII Madrid
Física
II Congreso de ingeniería espacial
Ingeniería
instituciones
Miguel Catalán
Movimiento
Theory of Dynamic Interactions
Theory of Dynamic Interactions
Blog de Física e Ingeniería de Tendencias21
Tendencias 21 (Madrid). ISSN 2174-6850
Tendencias 21 (Madrid). ISSN 2174-6850