El bamboleo se ha estimado en una variación de 0,7 segundos de arco en un período de 433 días, de tal forma que los polos de la Tierra oscilan, generando una circunferencia irregular de 3 a 15 metros de diámetro. Este movimiento se añade al de precesión de los equinoccios, y a los de nutación, rotación y traslación de la Tierra. Tradicionalmente no se ha podido justificar su origen, no obstante, en 2000 el Jet Propulsion Laboratory (Laboratorio de Propulsión a Chorro) de la NASA anunció que la supuesta causa principal del bamboleo de Chandler es la presión fluctuante del fondo oceánico, originada por los cambios en la temperatura y la salinidad, y por los cambios en la dirección de las corrientes oceánicas. No obstante, esta hipótesis todavía está en estudio por la comunidad científica
Ya publicamos trabajos de Arturo Rodriguez en estas páginas el pasado año:
https://www.tendencias21.net/fisica/Nuevos-avances-en-dinamica-rotacional-I_a79.html
https://www.tendencias21.net/fisica/Nuevos-avances-en-dinamica-rotacional-II_a80.html
Vamos a conocer la propuesta del ingeniero Arturo Rodriguez.
Introducción a la Teoría de Campos Giroscópicos
En el presente documento, vamos a describir una serie de ideas alternativas a la actualmente aceptada teoría del movimiento rotatorio basada en las ecuaciones de Euler. Dichas ideas van a permitir interpretar fenómenos observables, como es el llamado movimiento de Chandler que experimenta la tierra, como veremos mediante simulaciones por ordenador de las ecuaciones postuladas. Al mismo tiempo intentaremos demostrar que estas ideas coinciden con las expresadas en la “Teoría de Interacciones Dinámicas” (TID), a las que habríamos llegado por otros caminos, ya que nos hemos basado, al realizar el diseño del modelo matemático propuesto aquí, en el hecho de que debe existir una clara correspondencia entre la TID y nuestra propuesta, a la que llamaremos en adelante: “Teoría de Campos Giroscópicos” (TCG).
Hemos elegido este nombre porque se encuadra en el mismo marco que las ecuaciones de Navier-Stokes de la Dinámica de Fluidos. Es decir, nosotros no partimos de la cinemática del punto material de masa m, sino del concepto de partícula fluida de densidad ᵨ. A partir de aquí, hemos construido una teoría de campos basada en la aplicación de los operadores diferenciales característicos de estas teorías (el rotacional, la divergencia, etc…). Consideramos que la estructura matemática de la teoría no debe depender del estado de agregación de la materia que presente el objeto y que este se manifiesta solamente a través del valor de sus parámetros (viscosidad, etc…). Finalmente, integrando espacialmente las ecuaciones y teniendo en cuenta las condiciones de contorno que impone el objeto físico, se llegará a la solución del problema.
Teoría de Interacciones Dinámicas y Teoría de Campos Giroscópicos
La primera idea que vamos a introducir es la de “Inercia Rotacional”, ya postulada en la TID, donde ya está suficientemente descrita en la bibliografía. Es un concepto muy intuitivo si se está ya familiarizado con el equivalente para el movimiento lineal: la inercia de la materia, tal como la conocemos. Desde nuestro punto de vista, la incorporación de este concepto a la dinámica da lugar a la necesidad de separar el movimiento de rotación intrínseco, respecto a los otros movimientos reflejados en la cinemática descrita por los ángulos de Euler: la precesión y la nutación, ya que dicha inercia solo afectaría al primero. En nuestra teoría, no concebimos tal descomposición de movimientos, donde se parte de un único vector de velocidad angular y cuyas tres componentes corresponden a rotación, precesión y nutación, respectivamente.
Postulamos, por tanto, la existencia de dos vectores independientes: W y Ω, que serían perpendiculares entre sí. El primero corresponde a la rotación intrínseca y el segundo a la composición de los movimientos de precesión y de nutación. Estos dos vectores no se pueden sumar algebraicamente, de lo contrario volveríamos al modelo de ángulos de Euler. La única posibilidad que nos queda, es definir una estructura matemática en forma de función compleja: W + i Ω donde el primer término es Ω la parte real de la función y el segundo término representa la parte imaginaria, e i es raíz cuadrada de -1.
Esto podría parecer, en principio, un simple truco matemático sin ningún fundamento que lo sostenga. Veremos, a continuación, como el concepto de Holonomía (junto al concepto de simetría basada en Grupos de Lie) perteneciente a la geometría diferencial, va a suministrarnos los principios fundamentales para sostener nuestro modelo matemático.
El concepto de Holonomía se puede definir como una característica de la geometría diferencial que “mide como el transporte paralelo alrededor de lazos cerrados no preserva los datos geométricos que se transportan”. En nuestro caso, esta idea se identificaría con el ángulo formado por el vector tangente (es decir, la velocidad de la partícula) que forma consigo mismo después de haber sido transportado paralelamente 360 grados, correspondientes a un lazo cerrado (2π radianes). La Holonomía de la conexión puede ser identificada con un grupo de Lie, que podríamos denominar el “Grupo de Holonomía” de la teoría.
El grupo de Holonomía (o simplemente Grupo de Simetría) comúnmente aceptado en la cinemática de sólido rígido, descrita mediante ángulos de Euler, es el grupo de Lie SO (3), es decir, el grupo convencional de las rotaciones en tres dimensiones.
Ya publicamos trabajos de Arturo Rodriguez en estas páginas el pasado año:
https://www.tendencias21.net/fisica/Nuevos-avances-en-dinamica-rotacional-I_a79.html
https://www.tendencias21.net/fisica/Nuevos-avances-en-dinamica-rotacional-II_a80.html
Vamos a conocer la propuesta del ingeniero Arturo Rodriguez.
Introducción a la Teoría de Campos Giroscópicos
En el presente documento, vamos a describir una serie de ideas alternativas a la actualmente aceptada teoría del movimiento rotatorio basada en las ecuaciones de Euler. Dichas ideas van a permitir interpretar fenómenos observables, como es el llamado movimiento de Chandler que experimenta la tierra, como veremos mediante simulaciones por ordenador de las ecuaciones postuladas. Al mismo tiempo intentaremos demostrar que estas ideas coinciden con las expresadas en la “Teoría de Interacciones Dinámicas” (TID), a las que habríamos llegado por otros caminos, ya que nos hemos basado, al realizar el diseño del modelo matemático propuesto aquí, en el hecho de que debe existir una clara correspondencia entre la TID y nuestra propuesta, a la que llamaremos en adelante: “Teoría de Campos Giroscópicos” (TCG).
Hemos elegido este nombre porque se encuadra en el mismo marco que las ecuaciones de Navier-Stokes de la Dinámica de Fluidos. Es decir, nosotros no partimos de la cinemática del punto material de masa m, sino del concepto de partícula fluida de densidad ᵨ. A partir de aquí, hemos construido una teoría de campos basada en la aplicación de los operadores diferenciales característicos de estas teorías (el rotacional, la divergencia, etc…). Consideramos que la estructura matemática de la teoría no debe depender del estado de agregación de la materia que presente el objeto y que este se manifiesta solamente a través del valor de sus parámetros (viscosidad, etc…). Finalmente, integrando espacialmente las ecuaciones y teniendo en cuenta las condiciones de contorno que impone el objeto físico, se llegará a la solución del problema.
Teoría de Interacciones Dinámicas y Teoría de Campos Giroscópicos
La primera idea que vamos a introducir es la de “Inercia Rotacional”, ya postulada en la TID, donde ya está suficientemente descrita en la bibliografía. Es un concepto muy intuitivo si se está ya familiarizado con el equivalente para el movimiento lineal: la inercia de la materia, tal como la conocemos. Desde nuestro punto de vista, la incorporación de este concepto a la dinámica da lugar a la necesidad de separar el movimiento de rotación intrínseco, respecto a los otros movimientos reflejados en la cinemática descrita por los ángulos de Euler: la precesión y la nutación, ya que dicha inercia solo afectaría al primero. En nuestra teoría, no concebimos tal descomposición de movimientos, donde se parte de un único vector de velocidad angular y cuyas tres componentes corresponden a rotación, precesión y nutación, respectivamente.
Postulamos, por tanto, la existencia de dos vectores independientes: W y Ω, que serían perpendiculares entre sí. El primero corresponde a la rotación intrínseca y el segundo a la composición de los movimientos de precesión y de nutación. Estos dos vectores no se pueden sumar algebraicamente, de lo contrario volveríamos al modelo de ángulos de Euler. La única posibilidad que nos queda, es definir una estructura matemática en forma de función compleja: W + i Ω donde el primer término es Ω la parte real de la función y el segundo término representa la parte imaginaria, e i es raíz cuadrada de -1.
Esto podría parecer, en principio, un simple truco matemático sin ningún fundamento que lo sostenga. Veremos, a continuación, como el concepto de Holonomía (junto al concepto de simetría basada en Grupos de Lie) perteneciente a la geometría diferencial, va a suministrarnos los principios fundamentales para sostener nuestro modelo matemático.
El concepto de Holonomía se puede definir como una característica de la geometría diferencial que “mide como el transporte paralelo alrededor de lazos cerrados no preserva los datos geométricos que se transportan”. En nuestro caso, esta idea se identificaría con el ángulo formado por el vector tangente (es decir, la velocidad de la partícula) que forma consigo mismo después de haber sido transportado paralelamente 360 grados, correspondientes a un lazo cerrado (2π radianes). La Holonomía de la conexión puede ser identificada con un grupo de Lie, que podríamos denominar el “Grupo de Holonomía” de la teoría.
El grupo de Holonomía (o simplemente Grupo de Simetría) comúnmente aceptado en la cinemática de sólido rígido, descrita mediante ángulos de Euler, es el grupo de Lie SO (3), es decir, el grupo convencional de las rotaciones en tres dimensiones.
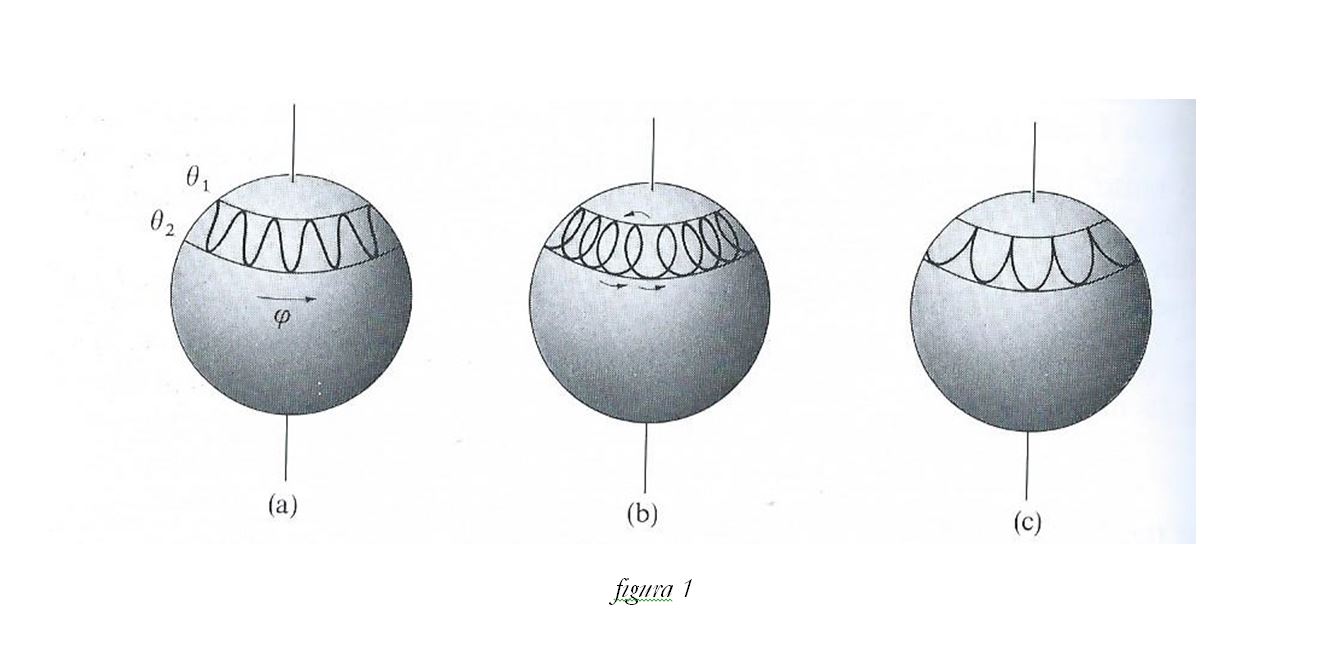
En nuestro modelo, este no es el grupo correcto, como se puede comprobar en la figura 2, que representa el movimiento de precesión y nutación de un giróscopo real, ya que la trayectoria del eje de rotación (para ser más exactos, su proyección a lo largo de una esfera, ver figura 1) no coincide con el observado en el experimento. Puede observase cierto desfase entre ambas curvas. Esto quiere decir que las herramientas geometro-diferenciales suministradas por SO (3), tal como se acepta en la actualidad, no son las adecuadas para describir el problema y será necesario, por tanto, postular un grupo de simetría más extenso y que lo contenga, al ser éste una buena aproximación al problema como lo demuestra el hecho de que su utilización en ciencia y tecnología está totalmente aceptado.
Nosotros lo que postulamos aquí es que el modelo de Euler, aun siendo útil en ingeniería (donde el movimiento de precesión está suprimido por el eje en la mayoría de los casos, como robots, etc…), no es el definitivo. Después de una serie de modificaciones en la estructura matemática del modelo descrito mediante el Lagrangiano del sistema, hemos llegado a la conclusión de que el verdadero grupo de Holonomía debería ser el SO (4) / Z2, donde Z2 representa el grupo de permutaciones de dos elementos y la barra representa el cociente entre los dos. Es interesante observar que a este grupo se le puede considerar como el que describe la simetría del problema de Kepler (ver página https://en.wikipedia.org/wiki/Laplace%E2%80%93Runge%E2%80%93Lenz_vector ). Veremos que esto va a permitir un marco conceptual adecuado a la hora de simular los movimientos simultáneos de rotación y órbitación alrededor del sol, producidos por la gravitación newtoniana, y que nos va a suministrar las herramientas necesarias para simular los movimientos de precesión y nutación de la tierra y, por tanto, el movimiento de Chandler.
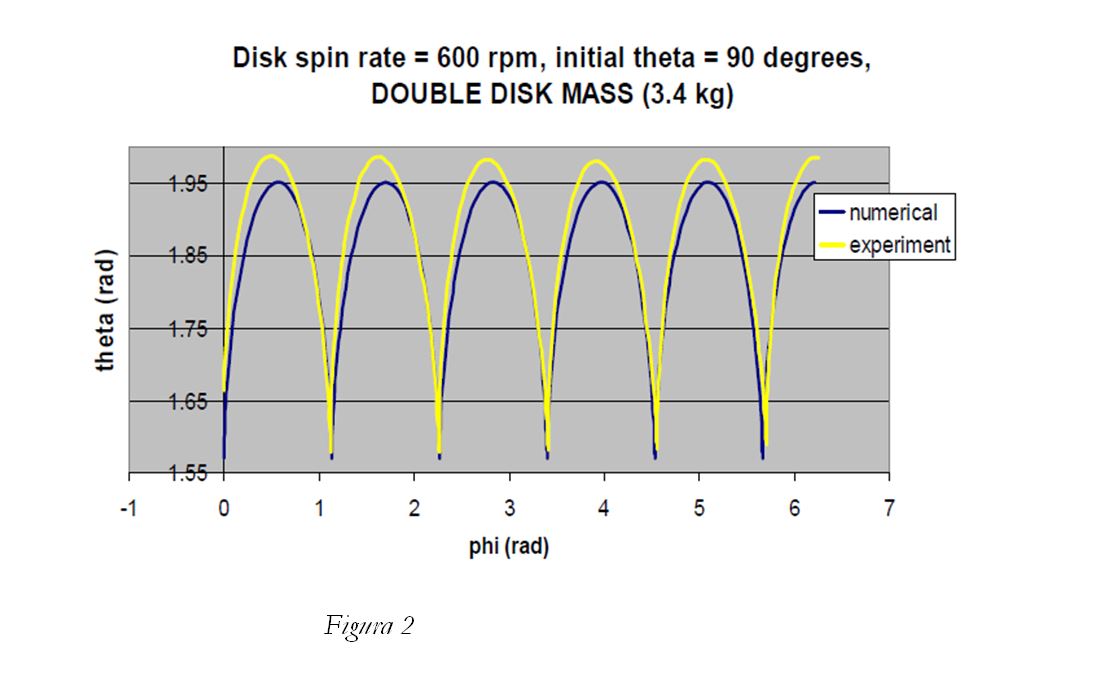
La siguiente figura, la cual hemos mencionado anteriormente, representa la variación del ángulo de nutación theta (θ) respecto del ángulo de precesión phi (ϕ), descritos ambos en la figura 1, obtenido en un experimento en el laboratorio. Como vemos el desfase obtenido entre el valor predicho por la teoría convencional (en azul) cuyo grupo de simetría es el SO (3) y el valor observado (en amarillo), aunque pequeño en apariencia, es reseñable ya que se deduce que, por acumulación del error, las curvas se desfasarán enormemente después de muchos ciclos. (En cursiva el texto original de Arturo Rodriguez)
Nosotros lo que postulamos aquí es que el modelo de Euler, aun siendo útil en ingeniería (donde el movimiento de precesión está suprimido por el eje en la mayoría de los casos, como robots, etc…), no es el definitivo. Después de una serie de modificaciones en la estructura matemática del modelo descrito mediante el Lagrangiano del sistema, hemos llegado a la conclusión de que el verdadero grupo de Holonomía debería ser el SO (4) / Z2, donde Z2 representa el grupo de permutaciones de dos elementos y la barra representa el cociente entre los dos. Es interesante observar que a este grupo se le puede considerar como el que describe la simetría del problema de Kepler (ver página https://en.wikipedia.org/wiki/Laplace%E2%80%93Runge%E2%80%93Lenz_vector ). Veremos que esto va a permitir un marco conceptual adecuado a la hora de simular los movimientos simultáneos de rotación y órbitación alrededor del sol, producidos por la gravitación newtoniana, y que nos va a suministrar las herramientas necesarias para simular los movimientos de precesión y nutación de la tierra y, por tanto, el movimiento de Chandler.
La siguiente figura, la cual hemos mencionado anteriormente, representa la variación del ángulo de nutación theta (θ) respecto del ángulo de precesión phi (ϕ), descritos ambos en la figura 1, obtenido en un experimento en el laboratorio. Como vemos el desfase obtenido entre el valor predicho por la teoría convencional (en azul) cuyo grupo de simetría es el SO (3) y el valor observado (en amarillo), aunque pequeño en apariencia, es reseñable ya que se deduce que, por acumulación del error, las curvas se desfasarán enormemente después de muchos ciclos. (En cursiva el texto original de Arturo Rodriguez)