Bitácora
Lunes, 9 de Junio 2008
Homenaje a Edgar Morin.
David Vilalta Murillo,
Miembro del Instituto de Ciencias de la Educación de la Universidad
Autónoma de Barcelona (UAB) y del grupo "La Cultura Matemática de las Personas".
Asesor de centros y coordinador de seminarios de escuelas de nueva
creación.

Hace un año, desde el Instituto de Ciencias de la Educación de la Universidad Autónoma de Barcelona, buscábamos personas con las que conversar. Tenemos la tarea de repensar la educación y queremos hacerla, también, en público, junto a trayectorias y prácticas exteriores a la educación. Para ello organizamos espacios donde imaginar sobre educación aportando la práctica docente de maestras de nuestros equipos y discursos con ecos sugerentes. En ese camino encontramos a Rafael Alberto Pérez y su nueva teoría estratégica. Así es que, como dice el refrán, de aquellos polvos estos lodos.
Y no diré que el azar nos presentó, porque hubo unas intenciones de búsqueda que, sin saberlo nosotros, nos acercaron. Este escrito viene a ser un recordatorio sintético, aunque reflexionado de mi escueta exposición en el Chateau d’Orion junto a los miembros de FISEC y el entrañable profesor Edgar Morin. Quisiera empezar esta aportación agradeciendo a Rafael y a las personas de FISEC su espíritu abierto, así como su cordialidad, generosidad y simpatía que han hallado un espacio en mi corazón.
Les voy a exponer, sucintamente, algunas de las ideas que desde el grupo la Cultura Matemática de las Personas venimos coconstruyendo. Somos maestras y maestros de educación infantil, primaria, secundaria y universidad, que dedicamos buena parte de nuestro tiempo a estudiar nuestras aulas, a leer y a comprendernos. En ese camino de más de ocho años hemos ido elaborando un discurso que nos permite seguir avanzando, a la vez que nos hace conscientes de lo que nos queda. Durante este tiempo hemos ido construyendo unas prácticas profesionales y unos argumentos para explicarlas y fundamentarlas cuyo modelo intentamos comprender.
Percibimos nuestra responsabilidad de maestros como el liderazgo de la formación emancipadora de personas y de sociedades orientadas a comprender el mundo y a comunicarse; también gestionamos las aulas como comunidades porque potenciamos los vínculos emocionales y el sentido de pertenecía a un grupo humano que está comprometido en una acción colectiva.
Lideramos estos procesos sin perder de vista que la escuela es una institución social que tiene que asegurar el éxito de su función específica: transmitir a las nuevas generaciones los elementos básicos de la herencia cultural.
Creemos que la transmisión de saberes básicos tiene éxito cuando se interpreta como un proceso de mediación cultural de los procesos emancipadores de formación de sociedades y de personas.
Como indica el nombre de nuestro grupo, las matemáticas juegan y han jugado un papel esencial en nuestro trabajo de construcción de nuestras prácticas y argumentos. Y creo que eso es así, porque ellas son una construcción cultural de la especie humana. Para nosotros, ese punto de vista es importante. Por poner un ejemplo, cuando la humanidad se ha encontrado con algún problema ha debido agudizar su empeño para encontrar soluciones. En ese ir y venir de problemas, soluciones o explicaciones se iban generando prácticas, herramientas, conjuntos de ideas, estrategias, muchas de ellas matemáticas. Pongamos por ejemplo la necesidad de saber cuantas cosas tengo. Esa necesidad para comerciar, para recabar impuestos, para prevenir… ha generado multitud de sistemas de contaje y a la postre de notación y numeración.
Somos conscientes que las matemáticas no van solas, y por ello hemos aprendido como se tiñen de complejidad nuestras aulas cuando descubrimos en los intereses y preocupaciones de los alumnos, oportunidades para la indagación así como para la alfabetización matemática y de otros saberes.
Y no diré que el azar nos presentó, porque hubo unas intenciones de búsqueda que, sin saberlo nosotros, nos acercaron. Este escrito viene a ser un recordatorio sintético, aunque reflexionado de mi escueta exposición en el Chateau d’Orion junto a los miembros de FISEC y el entrañable profesor Edgar Morin. Quisiera empezar esta aportación agradeciendo a Rafael y a las personas de FISEC su espíritu abierto, así como su cordialidad, generosidad y simpatía que han hallado un espacio en mi corazón.
Les voy a exponer, sucintamente, algunas de las ideas que desde el grupo la Cultura Matemática de las Personas venimos coconstruyendo. Somos maestras y maestros de educación infantil, primaria, secundaria y universidad, que dedicamos buena parte de nuestro tiempo a estudiar nuestras aulas, a leer y a comprendernos. En ese camino de más de ocho años hemos ido elaborando un discurso que nos permite seguir avanzando, a la vez que nos hace conscientes de lo que nos queda. Durante este tiempo hemos ido construyendo unas prácticas profesionales y unos argumentos para explicarlas y fundamentarlas cuyo modelo intentamos comprender.
Percibimos nuestra responsabilidad de maestros como el liderazgo de la formación emancipadora de personas y de sociedades orientadas a comprender el mundo y a comunicarse; también gestionamos las aulas como comunidades porque potenciamos los vínculos emocionales y el sentido de pertenecía a un grupo humano que está comprometido en una acción colectiva.
Lideramos estos procesos sin perder de vista que la escuela es una institución social que tiene que asegurar el éxito de su función específica: transmitir a las nuevas generaciones los elementos básicos de la herencia cultural.
Creemos que la transmisión de saberes básicos tiene éxito cuando se interpreta como un proceso de mediación cultural de los procesos emancipadores de formación de sociedades y de personas.
Como indica el nombre de nuestro grupo, las matemáticas juegan y han jugado un papel esencial en nuestro trabajo de construcción de nuestras prácticas y argumentos. Y creo que eso es así, porque ellas son una construcción cultural de la especie humana. Para nosotros, ese punto de vista es importante. Por poner un ejemplo, cuando la humanidad se ha encontrado con algún problema ha debido agudizar su empeño para encontrar soluciones. En ese ir y venir de problemas, soluciones o explicaciones se iban generando prácticas, herramientas, conjuntos de ideas, estrategias, muchas de ellas matemáticas. Pongamos por ejemplo la necesidad de saber cuantas cosas tengo. Esa necesidad para comerciar, para recabar impuestos, para prevenir… ha generado multitud de sistemas de contaje y a la postre de notación y numeración.
Somos conscientes que las matemáticas no van solas, y por ello hemos aprendido como se tiñen de complejidad nuestras aulas cuando descubrimos en los intereses y preocupaciones de los alumnos, oportunidades para la indagación así como para la alfabetización matemática y de otros saberes.
¿Qué queremos decir cuando decimos que intentamos entender el aula como un sistema social complejo adaptativo?
Para nosotros las aulas son grupos de personas. Pequeñas sociedades que los maestros debemos liderar para conseguir
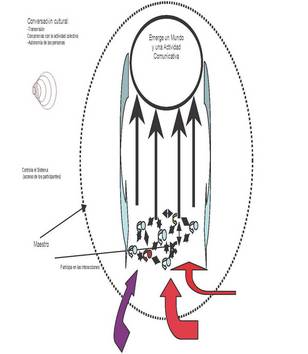
Figura 1
unas ciudadanas y ciudadanos con espíritu emprendedor y crítico, capacitados para tomar decisiones desde el conocimiento y sabiendo relacionar las “cosas”, unas personas implicadas con su entrono y solidarias.
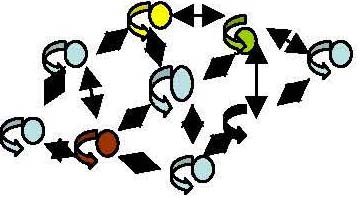
Como se puede observar en la figura 1, cada persona es diferente. La podríamos imaginar como un nudo en lo que sería la red de comunicaciones del aula. Cada persona (niño, niña, maestros) tienen una experiencia (la suya), una cosmovisión, unas maneras de hacer y de relacionarse… que pueden tener puntos de contacto entre los otros, pero también suelen presentar diferencias. Eso, en sí mismo ya lo consideramos una riqueza a explotar.
Procuramos que todo ese mundo de intereses, de ganas por conocer, de experiencias, que es cada persona entre en interacción simbólica con las demás. Para ello se precisa de un cierto orden entre la maraña de deseos, preocupaciones, maneras de hacer y constelaciones cognitivas de cada cual. Así pues, necesitamos generar un significado común sobre el sentido de lo que se hace en el aula, considerar que el significado de las cosas es fruto de una interacción social en la que las personas se ponen en el lugar del otro, con lo que cada uno puede verse a sí mismo como objeto y descubrir que el prójimo también tiene intenciones, y considerar que el significado de las cosas se manipula y modifica mediante procesos de interpretaciones. (1)
Poco a poco vamos construyendo junto al alumnado unas reglas de interacción basadas en darle sentido -para cada persona y para el grupo- a lo que se está haciendo, en compartir objetivos y elaborar planes de actuación, en ir encontrando sistemas de validación, temáticas relevantes y sistemas públicos de memoria colectiva.
Como indican las flechitas de la figura uno, esas interacciones provocan decisiones a dos niveles. A nivel personal, el hecho de acostumbrarme a discutir lo que se y lo que pienso con otros, con la intención de comprenderlos porque estoy implicado en lo que nos traemos entre manos; ese hecho provoca un conjunto de decisiones internas, personales que reconfiguran la identidad del individuo.
Es decir, se producen una serie de bucles de retroalimentación positiva; tantos como personas.
A su vez y a la vez, esos bucles están interaccionando con los demás, lo que genera un aula colmada de bucles interaccionando entre si, generando un segundo nivel de decisiones y significados.
Ahora bien, este sistema podría volverse trivial, en el sentido que dice el profesor Morin de “poder prevenir todos los comportamientos” y colapsarse. Para ello contamos con la diferencia de roles que juegan los maestros y los alumnos en ese cúmulo de flujos y bucles y también con la preocupación profesional por establecer buenas conexiones.
El rol de líder del maestro consiste en controlar el sistema para garantizar el acceso de todos los alumnos a la participación. Lo que no impide que también participe en los procesos de comunicación del aula.
De este modo, nuestras aulas van reflejando conexiones temáticas, conexiones de maneras de hacer, ideas…; propios y de los otros, tanto del interior del grupo como del exterior. Y al decir del exterior nos referimos al exterior más cercano o al más lejano ya des del punto de vista espacial como del temporal.
De todo ello emerge un modelo de relaciones entre las personas, con el conocimiento, una serie de actitudes y valores humanos. Ese modelo, a su vez, retroalimenta positivamente al sistema, incidiendo, de nuevo, en sus formas de relacionarse, en el tipo de temáticas, en la forma de abordarlas, en los sistemas de validación, en los planes de trabajo y objetivos…
Para nosotros las aulas son grupos de personas. Pequeñas sociedades que los maestros debemos liderar para conseguir
Figura 1
unas ciudadanas y ciudadanos con espíritu emprendedor y crítico, capacitados para tomar decisiones desde el conocimiento y sabiendo relacionar las “cosas”, unas personas implicadas con su entrono y solidarias.
Como se puede observar en la figura 1, cada persona es diferente. La podríamos imaginar como un nudo en lo que sería la red de comunicaciones del aula. Cada persona (niño, niña, maestros) tienen una experiencia (la suya), una cosmovisión, unas maneras de hacer y de relacionarse… que pueden tener puntos de contacto entre los otros, pero también suelen presentar diferencias. Eso, en sí mismo ya lo consideramos una riqueza a explotar.
Procuramos que todo ese mundo de intereses, de ganas por conocer, de experiencias, que es cada persona entre en interacción simbólica con las demás. Para ello se precisa de un cierto orden entre la maraña de deseos, preocupaciones, maneras de hacer y constelaciones cognitivas de cada cual. Así pues, necesitamos generar un significado común sobre el sentido de lo que se hace en el aula, considerar que el significado de las cosas es fruto de una interacción social en la que las personas se ponen en el lugar del otro, con lo que cada uno puede verse a sí mismo como objeto y descubrir que el prójimo también tiene intenciones, y considerar que el significado de las cosas se manipula y modifica mediante procesos de interpretaciones. (1)
Poco a poco vamos construyendo junto al alumnado unas reglas de interacción basadas en darle sentido -para cada persona y para el grupo- a lo que se está haciendo, en compartir objetivos y elaborar planes de actuación, en ir encontrando sistemas de validación, temáticas relevantes y sistemas públicos de memoria colectiva.
Como indican las flechitas de la figura uno, esas interacciones provocan decisiones a dos niveles. A nivel personal, el hecho de acostumbrarme a discutir lo que se y lo que pienso con otros, con la intención de comprenderlos porque estoy implicado en lo que nos traemos entre manos; ese hecho provoca un conjunto de decisiones internas, personales que reconfiguran la identidad del individuo.
Es decir, se producen una serie de bucles de retroalimentación positiva; tantos como personas.
A su vez y a la vez, esos bucles están interaccionando con los demás, lo que genera un aula colmada de bucles interaccionando entre si, generando un segundo nivel de decisiones y significados.
Ahora bien, este sistema podría volverse trivial, en el sentido que dice el profesor Morin de “poder prevenir todos los comportamientos” y colapsarse. Para ello contamos con la diferencia de roles que juegan los maestros y los alumnos en ese cúmulo de flujos y bucles y también con la preocupación profesional por establecer buenas conexiones.
El rol de líder del maestro consiste en controlar el sistema para garantizar el acceso de todos los alumnos a la participación. Lo que no impide que también participe en los procesos de comunicación del aula.
De este modo, nuestras aulas van reflejando conexiones temáticas, conexiones de maneras de hacer, ideas…; propios y de los otros, tanto del interior del grupo como del exterior. Y al decir del exterior nos referimos al exterior más cercano o al más lejano ya des del punto de vista espacial como del temporal.
De todo ello emerge un modelo de relaciones entre las personas, con el conocimiento, una serie de actitudes y valores humanos. Ese modelo, a su vez, retroalimenta positivamente al sistema, incidiendo, de nuevo, en sus formas de relacionarse, en el tipo de temáticas, en la forma de abordarlas, en los sistemas de validación, en los planes de trabajo y objetivos…
Ese modelo constituye un bucle de retroalimentación positiva, a otro nivel que los anteriores. Y lo dibujaríamos como una espiral en crecimiento porque constatamos como crecen las sociedades de nuestras aulas, las personas que en ellas
conviven y su compromiso con la actividad colectiva.
Precisamente, debido a la preocupación por la conexión con la herencia cultural de nuestra especie, consideramos que promovemos en nuestras aulas una conversación propia de la humanidad desde sus albores, que nos gusta denominar conversación cultural.
¿Objeto genético?
El cúmulo de interacciones así como de bucles de retroalimentación, permiten emergencias diversas, a veces imprevisibles o imprevistas, otras no. Por ejemplo, sabemos como tiñe los comportamientos de nuestros alumnos, ya desde bien pequeñitos el hecho de introducir una cinta métrica para hablar sobre algún fenómeno u objeto que les interesa. O como van cambiando comportamientos cuando se acostumbra a hablar utilizando información contrastada. O cuando se procura que los alumnos aprendan a establecer relaciones. O lo que supone que las personas sientan que saben.
Por ello nos atrevemos a decir que convivir con los demás, en determinadas condiciones “nos da a luz a nosotros mismos” (Maturana)(2) y a su vez genera unas aulas que rezuman una orientación básica y unas maneras de hacer que responden a un paradigma escolar nuevo. Tan diferentes son la orientación básica y las maneras de hacer de estas aulas del conjunto de comportamientos, convicciones e ideas que se viven mayoritariamente en las aulas.
Precisamente, debido a la preocupación por la conexión con la herencia cultural de nuestra especie, consideramos que promovemos en nuestras aulas una conversación propia de la humanidad desde sus albores, que nos gusta denominar conversación cultural.
¿Objeto genético?
El cúmulo de interacciones así como de bucles de retroalimentación, permiten emergencias diversas, a veces imprevisibles o imprevistas, otras no. Por ejemplo, sabemos como tiñe los comportamientos de nuestros alumnos, ya desde bien pequeñitos el hecho de introducir una cinta métrica para hablar sobre algún fenómeno u objeto que les interesa. O como van cambiando comportamientos cuando se acostumbra a hablar utilizando información contrastada. O cuando se procura que los alumnos aprendan a establecer relaciones. O lo que supone que las personas sientan que saben.
Por ello nos atrevemos a decir que convivir con los demás, en determinadas condiciones “nos da a luz a nosotros mismos” (Maturana)(2) y a su vez genera unas aulas que rezuman una orientación básica y unas maneras de hacer que responden a un paradigma escolar nuevo. Tan diferentes son la orientación básica y las maneras de hacer de estas aulas del conjunto de comportamientos, convicciones e ideas que se viven mayoritariamente en las aulas.

Un ejemplo: El viaje a la luna de unos niños y niñas de segundo de primaria.
Iñaki Villanueva es un maestro que sabe muy bien como generar en sus aulas procesos de indagación
rigurosos. Sus alumnos siempre suelen estar ocupados en investigaciones sobre metamorfosis de insectos, o descubriendo propiedades simétricas en las flores, incluso
encuentran series de Fibonacci en su entorno natural… En este caso, sus alumnos se sumergieron en la planificación y la realización de un viaje a la luna. Para ello tuvieron que enfrentar muchos retos. A Iñaki le gusta explicar cómo un día, leyendo un cómic de Tintín la viñeta que pueden ver aquí arriba les sumió en una profunda preocupación. En la viñeta unos operarios comentan:
- “¡Dios mío! ¡Si hubiéramos cometido un error en los cálculos! ¡Sería horroroso!”
- ¡Escuchad! ¡Escuchad! ¡Cohete que va a la Luna!
Esa preocupación por los cálculos les llevó a buscar sistemas para controlar que su cohete llegara al objetivo, para evitar que no pasara de largo y se perdiera por el espacio. Necesitaron informarse i comprender los movimientos de la Luna y de la Tierra, especularon sobre la trayectoria del cohete i sistemas para controlar la trayectoria.
Por motivos de tiempo me centraré en un episodio concreto, de todo el cúmulo de situaciones que se generaron en esa aula.
En esta clase, los alumnos están acostumbrados a que su maestro les proponga la construcción de modelos físicos para pensar sobre situaciones, para exponer ideas, con el objetivo de que se puedan visualizar las propuestas, favoreciendo su comprensión. El maestro les acostumbra a pensar sin barreras, a utilizar dibujos, información, instrumentos i materiales diversos. También están acostumbrados a realizar pequeñas indagaciones en grupos reducidos con el objetivo de presentar sus resultados al resto de la clase como una forma de aportar ideas en el proceso de resolver problemas de forma pública. Es este caso, los alumnos necesitaban construir una esfera (la Tierra) cuatro veces mayor que la otra (la Luna) porque necesitaban construir un modelo Tierra Luna que les permitiera pensar sobre la trayectoria del cohete cuando la Luna se mueve alrededor de la Tierra. Aparecieron diversas propuestas que enriquecieron mucho el debate i por tanto la comprensión de lo que se estaba tratando. Pero les quiero orientar su atención en el trabajo de este trio de alumnos, En el documento que elaboran para explicar sus propuestas, se puede observar una sensibilidad por el control del proceso. Dibujan la tierra y como saben que la Luna és quatro veces menor, además conocen el valor del diámetro de la Luna, dibujan y dividen el diámetro de la tierra en cuatro partes iguales. El dibujo les permite comprender la situación, dándoles seguridad para enfrentar el cálculo. La forma de calcular merecería un detenimiento pero lo vamos a saltar. Después de haber calculado, se produce una discusión entre los tres, que la consideran importante y por eso la escriben, escribiendo también su conclusión. Resulta que habían buscado en un libro y habían encontrado el diámetro de la Tierra, pero esa cantidad no correspondía con el resultado de sus cálculos.
Carlos: - “nos hemos equivocado”
Javi: - “quizá el del libro”
Víctor: - “la información no es correcta”
Y concluyen escribiendo y enmarcando el escrito:
“EN UN LIBRO QUE HEMOS MIRADO HABÍAN HECHO MAL LOS CÁLCULOS, HABÍAN PUESTO 12.756”
Resulta impresionante observar cómo emergen conductas, actitudes y significados sutiles y profundos, cuando los maestros encaran la complejidad de gestionar un grupo de personas haciéndolas protagonistas de sus procesos.
La naturaleza de los procesos matemáticos en nuestras aulas. (3)
Las matemáticas, como conocimiento, es una construcción cultural de los humanos con sus acciones instrumentales, sus estrategias, sus conceptos, sus contextos, su tecnología simbólica y sus problemas relevantes. Para nosotros el problema consiste en la transmisión de ese legado de forma emancipadora y creativa, porque sabemos que todo proceso de transmisión implica interpretación y porque nuestra misión es la educación de una ciudadanía libre, con criterios, preparada y solidaria con los problemas que nos afectan a todos.
Pero resulta que en la génesis misma de las matemáticas está la comunicación entre las personas y entre civilizaciones. “…ni el cero babilónico ni el maya fueron concebidos como un número: tan sólo el cero indio tuvo casi las mismas posibilidades que el que nosotros utilizamos hoy. Es el que nos ha sido transmitido por los árabes, al mismo tiempo que las cifras que llevan su nombre y que no son otras que las indias, un poco deformadas por el uso, el tiempo y los viajes.” Georges Ifrah (27, 2002) (4)
“…todavía cien años después (5) de publicado el Liber abaci, los banqueros florentinos tenían prohibido utilizarlas, tanto era el apego de los comerciantes italianos a sus viejas costumbres. Y en 1348 se aconsejaba a las autoridades académicas de Papua que exigiesen a los vendedores que el precio de los libros estuviera puesto en letras, no en cifras. Ricardo Moreno (61, 2004) (6)
Por este tipo de consideraciones, organizamos nuestras aulas como contextos de comunicación fluida; y por ello buscamos vínculos cotidianos e incrustamos las prácticas matemáticas entre sus dimensiones técnica, social y emancipadora.
rigurosos. Sus alumnos siempre suelen estar ocupados en investigaciones sobre metamorfosis de insectos, o descubriendo propiedades simétricas en las flores, incluso
encuentran series de Fibonacci en su entorno natural… En este caso, sus alumnos se sumergieron en la planificación y la realización de un viaje a la luna. Para ello tuvieron que enfrentar muchos retos. A Iñaki le gusta explicar cómo un día, leyendo un cómic de Tintín la viñeta que pueden ver aquí arriba les sumió en una profunda preocupación. En la viñeta unos operarios comentan:
- “¡Dios mío! ¡Si hubiéramos cometido un error en los cálculos! ¡Sería horroroso!”
- ¡Escuchad! ¡Escuchad! ¡Cohete que va a la Luna!
Esa preocupación por los cálculos les llevó a buscar sistemas para controlar que su cohete llegara al objetivo, para evitar que no pasara de largo y se perdiera por el espacio. Necesitaron informarse i comprender los movimientos de la Luna y de la Tierra, especularon sobre la trayectoria del cohete i sistemas para controlar la trayectoria.
Por motivos de tiempo me centraré en un episodio concreto, de todo el cúmulo de situaciones que se generaron en esa aula.
En esta clase, los alumnos están acostumbrados a que su maestro les proponga la construcción de modelos físicos para pensar sobre situaciones, para exponer ideas, con el objetivo de que se puedan visualizar las propuestas, favoreciendo su comprensión. El maestro les acostumbra a pensar sin barreras, a utilizar dibujos, información, instrumentos i materiales diversos. También están acostumbrados a realizar pequeñas indagaciones en grupos reducidos con el objetivo de presentar sus resultados al resto de la clase como una forma de aportar ideas en el proceso de resolver problemas de forma pública. Es este caso, los alumnos necesitaban construir una esfera (la Tierra) cuatro veces mayor que la otra (la Luna) porque necesitaban construir un modelo Tierra Luna que les permitiera pensar sobre la trayectoria del cohete cuando la Luna se mueve alrededor de la Tierra. Aparecieron diversas propuestas que enriquecieron mucho el debate i por tanto la comprensión de lo que se estaba tratando. Pero les quiero orientar su atención en el trabajo de este trio de alumnos, En el documento que elaboran para explicar sus propuestas, se puede observar una sensibilidad por el control del proceso. Dibujan la tierra y como saben que la Luna és quatro veces menor, además conocen el valor del diámetro de la Luna, dibujan y dividen el diámetro de la tierra en cuatro partes iguales. El dibujo les permite comprender la situación, dándoles seguridad para enfrentar el cálculo. La forma de calcular merecería un detenimiento pero lo vamos a saltar. Después de haber calculado, se produce una discusión entre los tres, que la consideran importante y por eso la escriben, escribiendo también su conclusión. Resulta que habían buscado en un libro y habían encontrado el diámetro de la Tierra, pero esa cantidad no correspondía con el resultado de sus cálculos.
Carlos: - “nos hemos equivocado”
Javi: - “quizá el del libro”
Víctor: - “la información no es correcta”
Y concluyen escribiendo y enmarcando el escrito:
“EN UN LIBRO QUE HEMOS MIRADO HABÍAN HECHO MAL LOS CÁLCULOS, HABÍAN PUESTO 12.756”
Resulta impresionante observar cómo emergen conductas, actitudes y significados sutiles y profundos, cuando los maestros encaran la complejidad de gestionar un grupo de personas haciéndolas protagonistas de sus procesos.
La naturaleza de los procesos matemáticos en nuestras aulas. (3)
Las matemáticas, como conocimiento, es una construcción cultural de los humanos con sus acciones instrumentales, sus estrategias, sus conceptos, sus contextos, su tecnología simbólica y sus problemas relevantes. Para nosotros el problema consiste en la transmisión de ese legado de forma emancipadora y creativa, porque sabemos que todo proceso de transmisión implica interpretación y porque nuestra misión es la educación de una ciudadanía libre, con criterios, preparada y solidaria con los problemas que nos afectan a todos.
Pero resulta que en la génesis misma de las matemáticas está la comunicación entre las personas y entre civilizaciones. “…ni el cero babilónico ni el maya fueron concebidos como un número: tan sólo el cero indio tuvo casi las mismas posibilidades que el que nosotros utilizamos hoy. Es el que nos ha sido transmitido por los árabes, al mismo tiempo que las cifras que llevan su nombre y que no son otras que las indias, un poco deformadas por el uso, el tiempo y los viajes.” Georges Ifrah (27, 2002) (4)
“…todavía cien años después (5) de publicado el Liber abaci, los banqueros florentinos tenían prohibido utilizarlas, tanto era el apego de los comerciantes italianos a sus viejas costumbres. Y en 1348 se aconsejaba a las autoridades académicas de Papua que exigiesen a los vendedores que el precio de los libros estuviera puesto en letras, no en cifras. Ricardo Moreno (61, 2004) (6)
Por este tipo de consideraciones, organizamos nuestras aulas como contextos de comunicación fluida; y por ello buscamos vínculos cotidianos e incrustamos las prácticas matemáticas entre sus dimensiones técnica, social y emancipadora.
David Vilalta Murillo
Instituto de Ciencias de la Educación de la UAB
La Cultura Matemática de las Personas
(0) Esquema Inspirado en un esquema de Chris Langton, Instituto de Santa Fe
(1) “El interaccionismo simbólico: Perspectiva y médodo”; H. Blumer. Hora SA;
(2)En La trama de la vida; F Kapra
(3) “Alfabetización matemática y comunidades escolares”; Carlos Gallego. Temps d¡Educació, Universitat de Barcelona. En prensa.
(4)Historia Universal de las Cifras, Georges Ifrah; Espasa Forum 2002
(5) El Liber abaci fue publicado en 1202
(6)Fibonacci. El primer matemático medieval. Ricardo Moreno Castillo; Nivela 2004
Instituto de Ciencias de la Educación de la UAB
La Cultura Matemática de las Personas
(0) Esquema Inspirado en un esquema de Chris Langton, Instituto de Santa Fe
(1) “El interaccionismo simbólico: Perspectiva y médodo”; H. Blumer. Hora SA;
(2)En La trama de la vida; F Kapra
(3) “Alfabetización matemática y comunidades escolares”; Carlos Gallego. Temps d¡Educació, Universitat de Barcelona. En prensa.
(4)Historia Universal de las Cifras, Georges Ifrah; Espasa Forum 2002
(5) El Liber abaci fue publicado en 1202
(6)Fibonacci. El primer matemático medieval. Ricardo Moreno Castillo; Nivela 2004
Editado por
Gabinete de Comunicación
El Foro Iberoamericano Sobre Estrategias de Comunicación (FISEC) es una asociación sin ánimo de lucro constituida en 2003 por un reducido grupo de académicos y expertos del mundo profesional de la Comunicación, con la intención de favorecer el intercambio más rico y productivo posible entre sus miembros, estudiosos, académicos y profesionales de la Comunicación Estratégica dentro del ámbito Iberoamericano.
Artículos de Fisec Estrategias
Enlaces
Archivo
Blog del Foro Iberoamericano sobre Estrategias de Comunicación en Tendencias21.
Envíenos un correo
Tendencias 21 (Madrid). ISSN 2174-6850
Envíenos un correo
Tendencias 21 (Madrid). ISSN 2174-6850