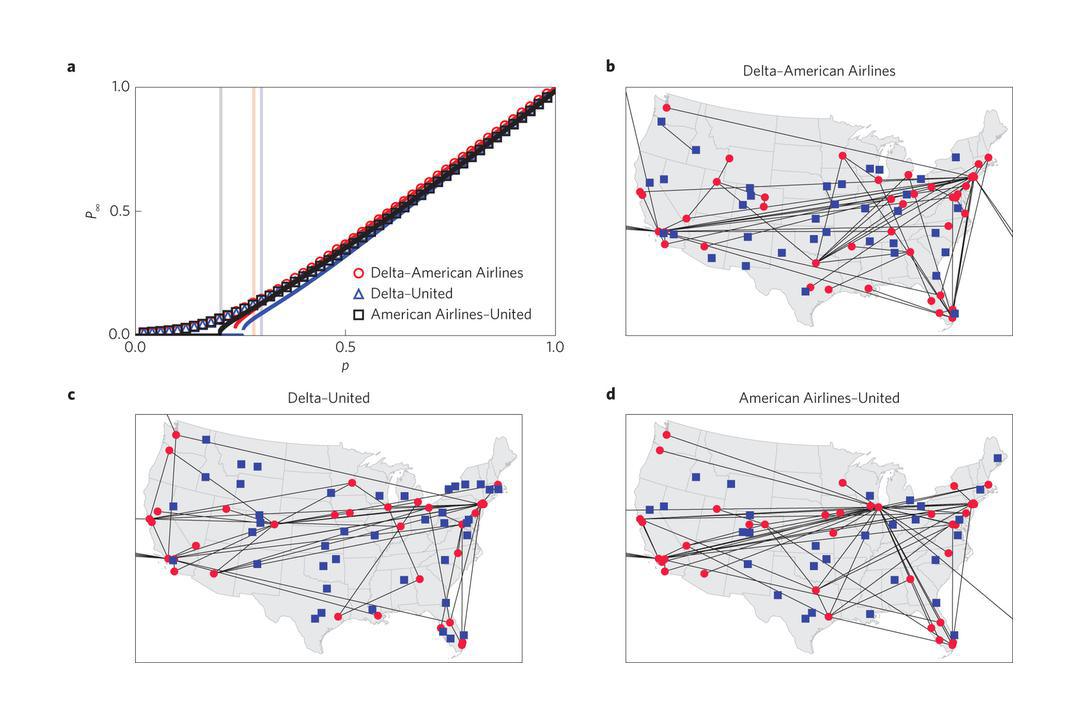
"Diagrama de percolación de grandes aerolíneas estadounidenses. Los aeropuertos en rojo y las conexiones entre ellos forman un "núcleo estructural" resistente a caídas del sistema. Imagen: Philippo Radicchi. Fuente: Universidad de Indiana.
Un investigador de la Universidad de Indiana (EE.UU.) ha desarrollado un nuevo marco matemático para analizar de manera más eficaz el "caos controlado", o cómo las interacciones entre los sistemas de alta complejidad afectan a su funcionamiento y vulnerabilidad.
El nuevo método podría ser utilizado para mejorar la capacidad de recuperación de los sistemas críticos complejos, como las redes de control de tráfico aéreo y las redes de energía, o retardar la propagación de amenazas a través de redes de gran tamaño, como los brotes de enfermedades.
"Al proporcionar resultados fiables de una manera rápida, estas ecuaciones permiten la creación de algoritmos que optimizan la resistencia de las redes interdependientes reales", dice en la nota de prensa de la universidad el autor del estudio, Filippo Radicchi, cuyo trabajo aparece en la revista Nature Physics.
"También pueden ser útiles en el diseño de sistemas complejos que sean más robustos, o más fácilmente recuperables", añade.
Radicchi es profesor de la Escuela de Informática y Computación y miembro del Centro de Redes Complejas y Sistemas de Investigación. Sus ecuaciones funcionan proporcionando un nuevo método para "desenredar" sistemas complejos múltiples, separando cada red, o "grafo", para su análisis individual; y luego la reconstrucción de una visión de conjunto.
Un "grafo" describe los innumerables puntos y líneas de conexión que forman una red compleja. En una red de transporte aéreo, por ejemplo, un aeropuerto podría representar un punto; la trayectoria de vuelo de un avión, las conexiones entre puntos.
"En el mundo real, no existen redes de manera aislada, sino que siempre están interactuando con otras redes", dice Radicchi. "Al desentrañar varios grafos, somos capaces de analizar cada uno aisladamente, proporcionando una imagen más completa de su interdependencia e interacción."
Las ecuaciones
La clave de la potencia de las ecuaciones es doble. En primer lugar, que no dependen de la utilización de simulaciones a gran escala, que son costosas y consumen mucho tiempo. En segundo lugar, son capaces de medir con rapidez y precisión la "percolación" de un sistema, un término que describe la cantidad de perturbaciones causadas por pequeñas averías en un sistema grande.
"Si va a viajar entre las ciudades en avión y el 10 por ciento de los aeropuertos de todo el mundo de repente dejar de funcionar por alguna razón, la teoría de la percolación puede ayudar a calcular cuántos aeropuertos podrá seguir utilizando para llegar a la ciudad de destino," explica Radicchi.
Una transición suave de percolación, según lo revelado a través de las ecuaciones, indica que un sistema dejará de funcionar gradualmente a medida que el número de fallos locales se eleve. Una transición brusca de percolación revela un sistema más propenso a dejar de funcionar de repente después de alcanzar un cierto número de fallos locales.
"En ese momento", dice Radicchi, "un sistema exhibirá" un comportamiento catastrófico "del que es muy difícil de recuperarse."
El nuevo método podría ser utilizado para mejorar la capacidad de recuperación de los sistemas críticos complejos, como las redes de control de tráfico aéreo y las redes de energía, o retardar la propagación de amenazas a través de redes de gran tamaño, como los brotes de enfermedades.
"Al proporcionar resultados fiables de una manera rápida, estas ecuaciones permiten la creación de algoritmos que optimizan la resistencia de las redes interdependientes reales", dice en la nota de prensa de la universidad el autor del estudio, Filippo Radicchi, cuyo trabajo aparece en la revista Nature Physics.
"También pueden ser útiles en el diseño de sistemas complejos que sean más robustos, o más fácilmente recuperables", añade.
Radicchi es profesor de la Escuela de Informática y Computación y miembro del Centro de Redes Complejas y Sistemas de Investigación. Sus ecuaciones funcionan proporcionando un nuevo método para "desenredar" sistemas complejos múltiples, separando cada red, o "grafo", para su análisis individual; y luego la reconstrucción de una visión de conjunto.
Un "grafo" describe los innumerables puntos y líneas de conexión que forman una red compleja. En una red de transporte aéreo, por ejemplo, un aeropuerto podría representar un punto; la trayectoria de vuelo de un avión, las conexiones entre puntos.
"En el mundo real, no existen redes de manera aislada, sino que siempre están interactuando con otras redes", dice Radicchi. "Al desentrañar varios grafos, somos capaces de analizar cada uno aisladamente, proporcionando una imagen más completa de su interdependencia e interacción."
Las ecuaciones
La clave de la potencia de las ecuaciones es doble. En primer lugar, que no dependen de la utilización de simulaciones a gran escala, que son costosas y consumen mucho tiempo. En segundo lugar, son capaces de medir con rapidez y precisión la "percolación" de un sistema, un término que describe la cantidad de perturbaciones causadas por pequeñas averías en un sistema grande.
"Si va a viajar entre las ciudades en avión y el 10 por ciento de los aeropuertos de todo el mundo de repente dejar de funcionar por alguna razón, la teoría de la percolación puede ayudar a calcular cuántos aeropuertos podrá seguir utilizando para llegar a la ciudad de destino," explica Radicchi.
Una transición suave de percolación, según lo revelado a través de las ecuaciones, indica que un sistema dejará de funcionar gradualmente a medida que el número de fallos locales se eleve. Una transición brusca de percolación revela un sistema más propenso a dejar de funcionar de repente después de alcanzar un cierto número de fallos locales.
"En ese momento", dice Radicchi, "un sistema exhibirá" un comportamiento catastrófico "del que es muy difícil de recuperarse."
Ejemplo
Como ejemplo tristemente famoso de infraestructura inestable, Radicchi apunta a un apagón masivo en su país natal, Italia, en 2003, en el que la red eléctrica de toda la nación colapsó en cuestión de minutos.
El problema se remonta al control de los generadores de energía de la nación, que era dependiente de una red de telecomunicaciones, que, ella misma, no podía funcionar adecuadamente sin electricidad.
"Cuando se fue la luz, los routers de telecomunicaciones también fallaron, provocando más caos y anulando también la red de comunicaciones de Internet", dice. "Estos son los tipos de situaciones que debemos ser capaces de detectar antes de que ocurran, no después de que sea demasiado tarde."
En términos de infraestructura, dice Radicchi que los mismos métodos utilizados para detectar vulnerabilidades en una red de transporte también podrían ayudar a crear planes para reducir los costes de construcción o acortar los tiempos de viaje. O podrían ser aplicados a comprender mejor otros sistemas complejos que permanecen sorprendentemente resistente al análisis, tales como el cuerpo humano, el cerebro y las redes sociales.
"También Podemos ser capaces de optimizar aún más estos sistemas", agregó. "Por ejemplo, impulsndo la difusión de los nuevos conocimientos y las ideas."
Como ejemplo tristemente famoso de infraestructura inestable, Radicchi apunta a un apagón masivo en su país natal, Italia, en 2003, en el que la red eléctrica de toda la nación colapsó en cuestión de minutos.
El problema se remonta al control de los generadores de energía de la nación, que era dependiente de una red de telecomunicaciones, que, ella misma, no podía funcionar adecuadamente sin electricidad.
"Cuando se fue la luz, los routers de telecomunicaciones también fallaron, provocando más caos y anulando también la red de comunicaciones de Internet", dice. "Estos son los tipos de situaciones que debemos ser capaces de detectar antes de que ocurran, no después de que sea demasiado tarde."
En términos de infraestructura, dice Radicchi que los mismos métodos utilizados para detectar vulnerabilidades en una red de transporte también podrían ayudar a crear planes para reducir los costes de construcción o acortar los tiempos de viaje. O podrían ser aplicados a comprender mejor otros sistemas complejos que permanecen sorprendentemente resistente al análisis, tales como el cuerpo humano, el cerebro y las redes sociales.
"También Podemos ser capaces de optimizar aún más estos sistemas", agregó. "Por ejemplo, impulsndo la difusión de los nuevos conocimientos y las ideas."
Referencia bibliográfica:
Filippo Radicchi: Percolation in real interdependent networks. Nature Physics (2015). DOI:10.1038/nphys3374.
Filippo Radicchi: Percolation in real interdependent networks. Nature Physics (2015). DOI:10.1038/nphys3374.